Vidéo introductive
Notion d'images numériques
Dans cette séance on s'intéresse aux images numériques.
On définira la notion de pixels et la façon dont sont représentés les pixels d'une image couleur.
On parlera également de la définition et de la profondeur de couleur d'une image numérique, mais aussi de la résolution et de la taille d'une image.
Des pixels.
Crédits : BlueEel at Danish Wikipedia, CC BY-SA 3.0, via Wikimedia Commons.
Définition d'une image
Une image numérique est juste la juxtapostion de petits carrés(ensemble de points) appelés pixels.
Voici à titre d'exemple :
le signe du langage Python et un agrandissement


Ou encore une image du Golden Gate :



La définition d'une image est le nombre de pixels constituant l'image. Cette définition est souvent donnée sous la forme où et sont les nombres de pixels de l'image en largeur et en hauteur. Par exemple, une image 4000 x 3000 a une définition de 12 000 000 pixels soit 12 megapixels.
✏️ À faire
Cliquez ici pour accéder à une image sur une banque d'images, puis répondez aux questions ci-dessous.
✍️ Question 1 : Quelle est la licence de cette image ? Expliquez ce que cela signifie.
✍️ Question 2 : Cliquez en bas à droite sur l'icône "Télécharger" puis sélectionnez "Affichez toutes les tailles" (le mot "taille" est par ailleurs mal choisi car il désigne autre chose, voir plus bas). Quelle est la définition la plus élevée pour cette image (celle prise par l'appareil photo numérique) ?
✍️ Question 3 : Quelle est la définition de la version "miniature" ?
Comment un écran affiche-t-il des pixels ?
L'observation à la loupe de différents écrans de smartphone donne ceci :

On peut constater des différences dans l’agencement ou la forme des pixels (et sous-pixels), suivant le modèle de smartphone observé :
Concrếtement, quelle est la taille(on dit le pas) des pixels sur un écran ?
Ca dépend de la qualité de l'écran.
En gros, le pas d'un pixel varie de 0,31 mm à 0,21 mm.
Les sous-pixels sont donc 3 fois plus fins.
Le principe est bien qu'un oeil humain ne puisse pas distinguer les sous-pixels en étant à une distance d'utilisation typique.
Pour afficher une image sur un écran de smartphone, seules trois couleurs sont donc disponibles : le rouge, le vert et le bleu. Comment ces 3 couleurs peuvent-elles générer toutes les autres couleurs ?
Les pixels d'une image et leur codage
Le codage RVB
La couleur d'un pixel est représenté par trois valeurs : celle du rouge (R), celle du vert (V) et celle du bleu (B).
En effet, en "mélangeant" une certaine intensité de chacune de ses trois couleurs, on peut obtenir toutes les couleurs, c'est le principe physique de la synthèse additive des couleurs.

Schéma de la synthèse additive des couleurs.
Pour mémoriser une image, il suffit de mémoriser chacun de ses pixels. Comme un pixel est définit par ses 3 composantes R, V et B, il suffit de mémoriser ces trois valeurs pour chaque pixel.
La profondeur de couleur d'une image est le nombre de bits utilisés pour coder la couleur d'un pixel. Les images couleur classiques ont une profondeur 24 bits (3 octets), c'est-à-dire que chaque composante R, V et B est codée sur 8 bits (1 octet), donc par un nombre entier compris entre 0 et 255. Ainsi, on peut donner la couleur d'un pixel par un triplet , par exemple qui signifie que , et .
Plus la profondeur de couleur est élevée, plus la palette de couleurs possibles est grande ! Néanmoins, une profondeur de couleur de 24 bits est largement suffisante la plupart du temps.
✍️ Question 4 : On dispose une image dont la définition est 1024 * 768 et dont la profondeur de couleur est 24 bits. Calculer la taille, en octet, du fichier correspondant à cette image.
Pouvoir séparateur de l'oeil
Notre oeil ne peut pas le voir, mais lorsque l'on observe le pixel d'un écran (d'ordinateur, de smartphone, de TV, etc.) à la loupe, on peut constater qu'il est constitué de trois parties : une partie rouge, une partie verte et une partie bleue comme sur la photo ci-dessous.
Écran d'un smartphone affichant la couleur blanche.
Crédits : Dinesh Dhankhar, Licence CC BY 4.0.
Pourquoi notre oeil ne peut pas le voir ? Car il est limité par son pouvoir séparateur ! Deux points trop proches l'un de l'autre ne peuvent pas être distingués l'un de l'autre par notre oeil, qui les superposera. Par exemple, si vous vous éloignez de votre écran, les trois images ci-dessous sembleront identiques à partir d'un certaine distance.

Trois images d'une voiture, d'une haute résolution à une basse résolution.
Crédits : Thegreenj~commonswiki supposé (étant donné la revendication de droit d’auteur)., CC BY-SA 3.0, via Wikimedia Commons.
Le pouvoir séparateur de l'oeil s'appelle aussi le pouvoir de résolution. Nous parlerons par la suite de la résolution d'une image qui ne doit pas être trop petite, au risque de voir cette image pixélisée.
✏️ À faire
L'application proposée sur ce site permet d'obtenir différentes couleurs en faisant varier les canaux rouge, vert et bleu (à l'aide des boutons + et - ou en sélectionnant une couleur nommée). Utilisez ce site pour répondre aux questions qui suivent.
✍️ Question 5 : Quelles valeurs des canaux (décimal RGB) permettent d'obtenir :
- d'obtenir du rouge (pur) ?
- d'obtenir du blanc ?
- d'obtenir du noir ?
- d'obtenir du jaune (pur) ?
- d'obtenir du cyan ?
✍️ Question 6 : Que se passe-t-il quand les trois canaux ont la même valeur (par exemple (125,125,125) ou (50, 50, 50)) ?
✍️ Question 7 : Combien de couleurs différentes est-il possible d’obtenir avec ce système RVB (pour une profondeur de couleur 24 bits comme c'est le cas ici) ? Expliquez.
Résolution d'une image
La taille d'une image (ou dimension) correspond à ses dimensions physiques (largeur*hauteur) en pouce, qui est une unité de longueur anglophone.
Un pouce est égal à 2,54 cm, son symbole est « " »
La résolution d'une image est le nombre de pixels par pouce, exprimée communément en pixels par pouce (ppp) à l’écran ou en points par pouce (ppp) pour l’impression.
Concrètement, la résolution est donc le nombre de pixels présents sur un pouce de longueur.
La résolution se calcule à partir de la définition et de la taille en utilisant l'une des deux formules suivantes :
Remarques :
- Pour une taille fixée, plus la résolution est élevée plus la qualité l'est. Des résolutions trop faibles entraînent un phénomène de pixellisation ;
- ⚠️ La résolution ne doit pas être confondue avec la définition d'une image, ce n'est pas une caractéristique du fichier image.
Elle ne peut pas être calculée sans connaître la taille du support.
Malheureusement, on retrouve cette confusion quasiment partout ... ; - On rencontre aussi souvent les unités pixel per inch (ppi) et dots per inch (dpi) qui sont les traductions anglaises de pixels par pouce et points par pouce.
Souvent la taille d'un écran est donnée par la longueur de sa diagonale (en pouce).
Exemple : Calcul de la résolution du Fairphone 5

Le Fairphone 5
Crédits : Fairphone, licence CC BY-SA, via Flickr.
Les caractéristiques techniques du Fairephone 5 permettent de trouver les informations suivantes sur son écran :
- Définition : 2770 x 1224 pixels
- Taille de l'écran : 15.33 x 6.77 cm
Quelle est la résolution de l'écran, en pixels par pouce ?
On raisonne soit avec la hauteur, soit avec largeur. Prenons par exemple la hauteur :
- Elle vaut 15.33 cm donc environ 6.04" (car ).
- Donc il y a 2770 pixels sur une longueur de 6.04"
- Sa résolution se calcule donc ainsi : ppp.
Le Fairphone 5 a donc un écran qui permet d'afficher 459 pixels sur une longueur de 1 pouce (sur 2,54 cm).
On trouverait le même résultat en travaillant avec la largeur.
Quelle est la largeur (le pas) d'un pixel de cet écran ?
Comme un pouce correspond à D = 2,54 cm = 25,4 mm, on peut trouver facilement la largeur L théorique du pixel : D = resolution x L
On trouve la largeur L d'un pixel en calculant L = D / resolution
La largeur d'un pixel se calcule donc ainsi : mm.
Le Fairphone 5 a donc un écran qui permet d'afficher 459 pixels sur une longueur de 1 pouce, chaque pixel a un pas d'environ 0.055 mm.
✍️ Question 8 : Chacune des figures suivantes représente une image imprimée, un carré représentant un pixel. Pour chaque image, déterminez sa taille (en pouces), sa définition (en pixels) et sa résolution (en ppp).

Source : Extrait du cahier d'activités de SNT de Nathan, page 93.
✍️ Question 9 : Repérez les deux imprécisions/erreurs de vocabulaire dans les caractéristiques de l'iPhone 13 données par le site de vente en ligne Cdiscount.
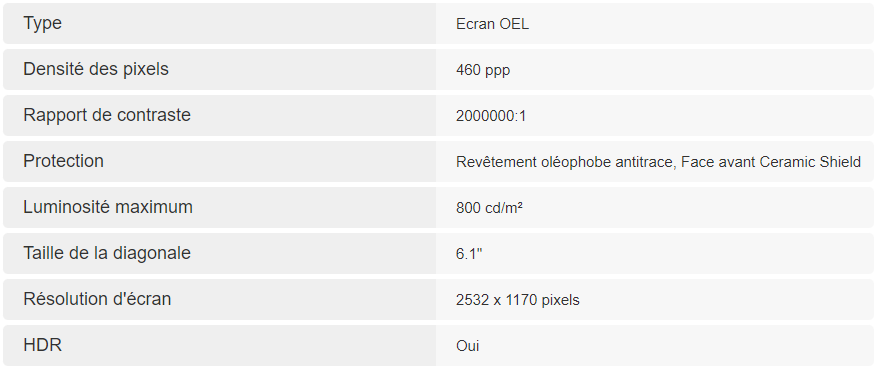
Source : Cdiscount.
Exercices
Exercice 1
- Mesurez la largeur et la hauteur de l’écran de votre smartphone et convertissez ces mesures en pouces.
- Cherchez la définition de l’écran de votre smartphone (vous pouvez trouver cette information sur le Web ou dans les paramètres de votre téléphone).
- Calculez alors la résolution de votre écran en ppp (pixels par pouce). Comparez votre résultat avec les informations trouvées sur le Web.
Exercice 2
- L'écran d'un smartphone a une résolution de 458 ppp et affiche des images de définition 2436 x 1125.
Calculez la taille de cet écran (largeur, hauteur) en cm. - Déterminer la largeur d'un pixel pour l'écran d'un galaxy S20+ qui affiche 525 dpi.
Exercice 3
À l'impression, on estime qu’une image est de bonne qualité si sa résolution est supérieure à 300 ppp (points par pouces). Alban a pris une photo dont la définition est 1920 × 2560 pixels. Il souhaite imprimer cette photo dans le plus grand format possible mais que le résultat soit de bonne qualité.
- Calculez la résolution de cette image si on l'imprime au format 9 x 12 cm, au format 12 x 16 cm et au format 18 x 24 cm.
- Que lui conseillez-vous ?
Modification :
Andjekel
Références :
- Les enseignants de SNT du lycée Mounier, ANGERS
- David Roche, lien vers la séance : https://pixees.fr/informatiquelycee/n_site/snt_photo_image.html
- Article Wikipédia sur le pouvoir de résolution.
- Manuel de SNT de Bordas.
- Cahier d’activités de SNT de Nathan.