NSI Terminale

C1 Recursivité - TP

Travaux Pratiques

▪ TP 1 : Flocon de Von Koch 

La courbe de Koch est une figure qui se construit de manière récursive. Le cas de base (ordre 0) s'obtient en traçant un segment de longueur l. Le cas récursif d'ordre n>0 s'obtient en effectuant les transformations suivantes :

Etape Illustration Commentaire
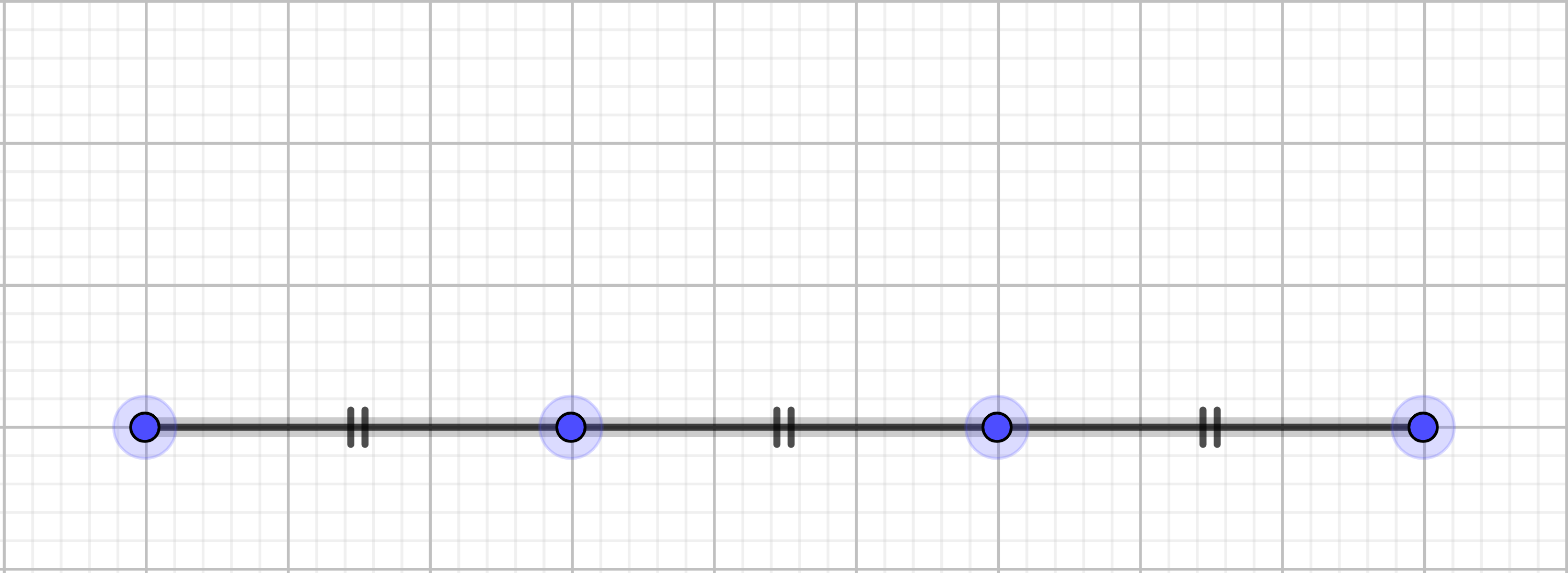1⃣ koch1 Partager le segment en trois morceaux de longueur égale
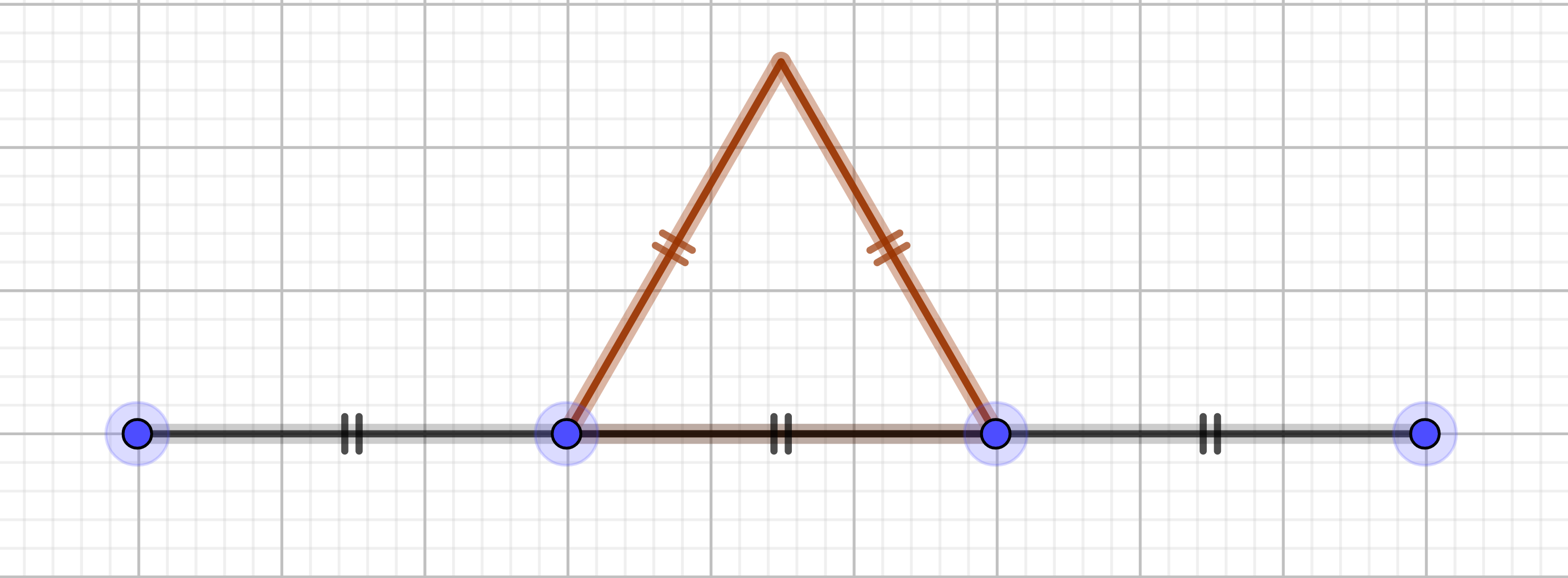2⃣ koch2 Construire un triangle équilatéral à partir du segment du milieu
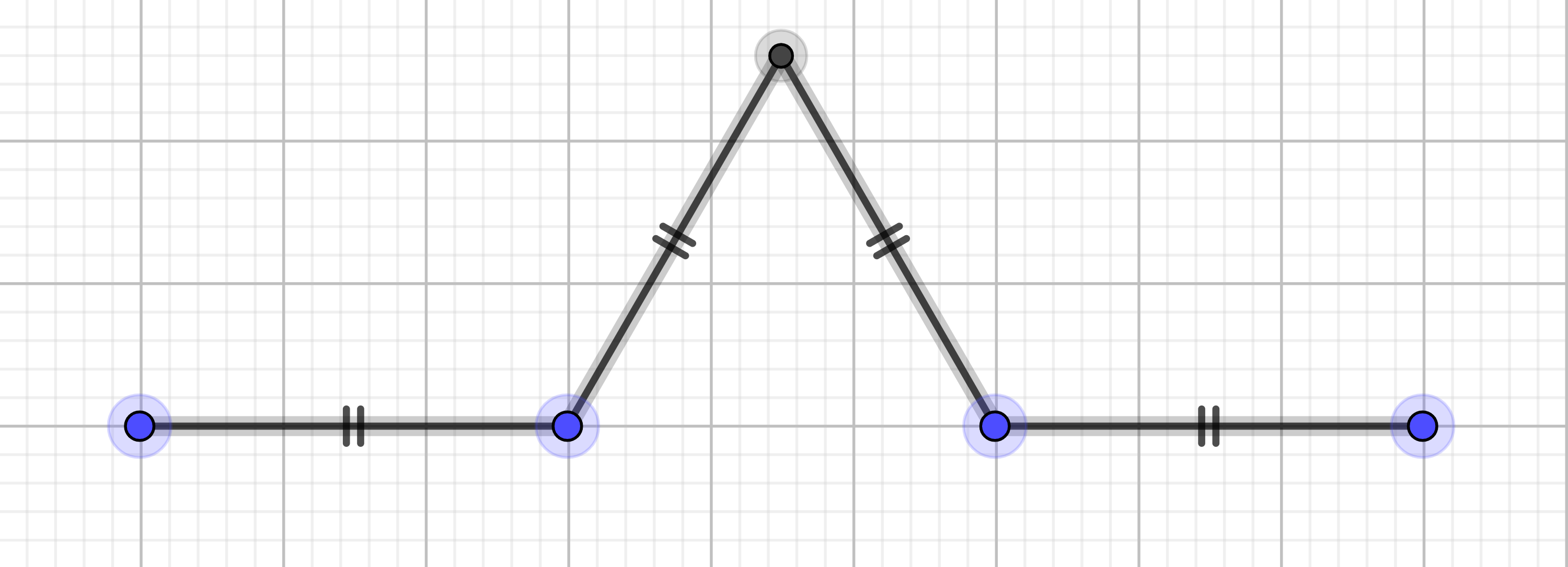3⃣ koch3 Supprimer le segment du milieu

On a écrit une fonction courbe_koch permettant de tracer à l'aide du module turtle de Python la courbe de Koch en donnant en paramètre la longueur initiale du segment et l'ordre. On donne ci-dessous ce code incomplet : 

def courbe_koch(tortue,longueur,ordre):
    if ........
        ........
    else:
        ordre=........
        longueur=........
        courbe_koch(tortue,longueur,ordre)
        .................
        courbe_koch(tortue,longueur,ordre)
        ................
        courbe_koch(tortue,longueur,ordre)
        ................
        courbe_koch(tortue,longueur,ordre)

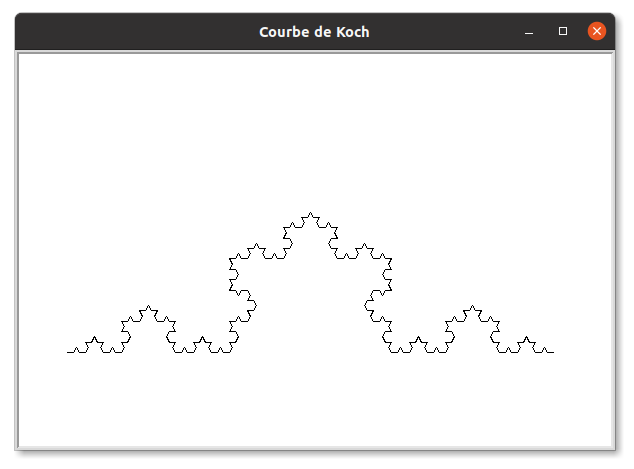
  1. Compléter et tester ce code pour tracer une courbe de Koch d'ordre 4. Vous devriez obtenir une figure similaire à celle représentée ci-dessous : courbekoch
  2. En utilisant cette fonction construire le flocon de Koch, c'est à dire la figure obtenu en construisant les courbe de Koch sur les trois côtés d'un triangle équilatéral.
  3. Le flocon de Koch est un exemple classique de courbe fractale, construire un autre exemple de fractale : le triangle de Sierpinski.

▪ TP 2 : Les tours de Hanoï

Inventé par le mathématicien français Edouard Lucas, les tours de Hanoï sont un jeu de réflexion dans lequel on doit déplacer des disques de tailles croissantes d'une tour de départ à une tour d'arrivée en respectant les contraintes suivantes :
on ne peut déplacer qu'un disque à la fois, celui situé en haut de la tour
on ne peut jamais déplacer un disque sur un disque plus petit.

  1. Faire quelques parties en ligne à cette adresse pour comprendre le jeu.
  2. Module hanoi.py
    1. Télécharger ci-dessous le module Python Hanoi.py et le sauver dans le répertoire de votre choix. Module Hanoi
    2. Ce module propose les fonctions suivantes :
      dessine_depart(n) qui dessine l'état de départ du jeu avec n disques.
      fin() affiche dans la fenêtre "Cliquer pour terminer" et termine le programme après un clic.
      deplace_disque(depart,arrive) déplace le disque de la tour depart à la tour arrivee si cela est possible (sinon affiche un message d'erreur).
      On donne ci-dessous un exemple d'utilisation de ce module, le compléter de façon à afficher la résolution complète du jeu avec 3 disques. 
          import hanoi

    hanoi.dessine_depart(3)
    hanoi.deplace_disque(1,3)
    hanoi.fin()

  3. Résolution automatique par récursivité

    1. Compléter la description de chacune des étapes de la résolution du problème pour 6 disques illustrées ci-dessous :
    Etape Illustration Descriptions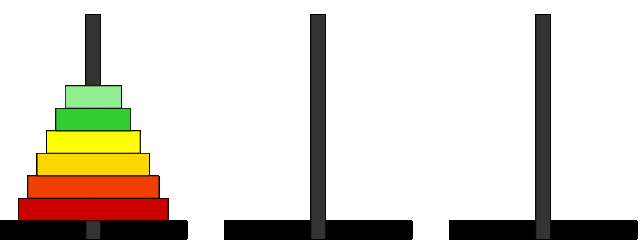
    0⃣ hanoi0 6 disques empilés sur la tour 1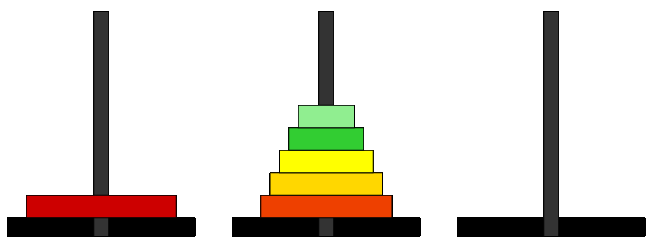
    1⃣ hanoi1 Déplacement de ... disques de la tour 1 vers la tour ....
    2⃣ hanoi2 Déplacement du disque de la tour ... vers la tour ...
    3⃣ hanoi3 Déplacement de ... disques de la tour 1 vers la tour ....
    1. Exprimer les étapes 1 et 3 sous la forme de la résolution d'un problème de tours de Hanoi dont on précisera la tour d'arrivée, la tour de départ ainsi que le nombre de disque.

    2. Compléter :

      Pour résoudre hanoi à 6 disques :
      Résoudre hanoi à ... disques
      Déplacer le disque de taille 6
      Résoudre hanoi à ... disques

    3. En déduire un algorithme récursif pour résoudre le problème des tours de Hanoï.

    4. Coder et faire fonctionner cet algorithme à l'aide des fonctions présentes dans le module hanoi.py.