Liste - TD Cours et applications simples -
Compléments

L'an dernier, vous avez vu la différence entre un algorithme et son implémentation concrète en programme : un même algorithme peut être traduit par un programme dans différents langages ou même en différentes versions de programmes pour un même langage. Tant que les programmes vont la même chose, l'utilisateur ne verra pas la différence.
Or, un algorithme manipule des données. Nous ne pouvons donc pas rattacher notre algorithme abstrait à des données concrètes en machine !
Vous allez donc comprendre aujourd'hui une nouvelle notion fondamentale en informatique.
Nous allons cette année faire la même chose pour les données : nous attarder sur les types abstraits de données qu'on retrouve dans la plupart des problèmes que l'informatique tente de résoudre. Et nous verrons qu'on peut les implémenter en machine sous différentes structures de données.
Ainsi,
- un algorithme manipule des types abstraits de données (c'est la phase de conception théorique)
- le passage de l'idée abstraite à sa réalisation concrète en machine se nomme l'implémentation.
- un programme manipule des structure de données (c'est la phase de réalisation pratique).
ALGORITHME ⇒ Implémentation ⇒ PROGRAMME
TYPE ABSTRAIT ⇒ Implémentation ⇒ STRUCTURE DE DONNEES
Variantes : plutôt que structure de données, on parle aussi de type concret ou même de type tout court. En réalité, l'utilisation du mot "structure de données" englobe parfois un peu les deux : le type abstrait et le type concret puisque pour concevoir la structure de données concrétement, il faut savoir ce qu'on veut de façon abstraite.
En réalité, ce n'est pas vraiment nouveau pour vous :
- La plupart des algorithmes de 1er utilisaient des tableaux statiques (un type abstrait de données).
- Or, nous avons créé des programmes Python qui implémentent ces tableaux en utilisant le type concret list de Python (une structure de données concrète).
1 - La Liste en tant que type abstrait de données
On peut travailler sur des données organisées de façon purement théorique, répondant à des contraintes théoriques, sans se soucier de la façon dont elles vont être concrétement programmées en interne par votre programme.
Rappel
1) Définition du type abstrait Liste : leurs propriétés générales
1a) Propriétes générales d'organisation
Le type abstrait Liste a les propriétés suivantes :
- elle est composée d'une séquence finie et ordonnée d'éléments : quelque soit l'élément en cours de lecture, on doit pouvoir trouver l'élément suivant. Partant du premier, on doit donc pouvoir se diriger linéairement jusqu'au dernier, sans ambiguïté.
- on peut accéder librement à n'importe quel élément de la liste
- on peut rajouter ou supprimer des éléments à n'importe quelle position
Finalement, vous pouvez appréhender le type abstrait Liste en faisant une analogie avec des dossiers suspendus :

1b) Vocabulaire
- On désigne le premier élément de la liste sous le nom de tête (head en anglais). On ordonne les éléments à partir de cette tête.
- Le reste des éléments de la liste porte le nom de queue (tail en anglais). Il s'agit donc de l'ensemble des éléments exceptée la tête.
- Si tous les éléments stockés sont de même type, on dit que la Liste est homogène, sinon elle est inhomogène.
1c) Exemple
Deux façons de voir graphiquement une liste contenant une tête valant 5 suivie d'une queue valant 8, 2 et 3.
- 5 → 8 → 2 → 3
- 3 ← 2 ← 8 ← 5

1d) Propriétés mathématiques ?
Le choix a été fait ici de définir les propriétés sous forme de phrases informelles.
On pourrait formaliser tout cela de façon rigoureuse et établir précisement toutes les propriétés mathématiques que doit avoir le type Liste.
Avantage de la définition globale : facile à comprendre.
Désavantage de la définition globale : pas de formalisme mathématique, les preuves et démonstration manquent de rigueur.
01° Quel élément forme ici la tête ? Quelle est la séquence qui forme la queue Que contient au total la Liste ?
12 → 4 → 5 → -15
...CORRECTION...
La tête est ici identifiée par la couleur ET le sens des flèches.
La tête contient donc 12.
La queue est donc composée de la séquence (4, 5, -15).
La liste complète est donc (12, 4, 5, -15).
02° Quel élément forme ici la tête ? Quelle est la séquence qui forme la queue ? Que contient au total la Liste ?
23 ← 12 ← 460 ← 1
...CORRECTION...
La tête est ici identifiée par la couleur ET le sens des flèches.
La tête contient donc 1.
La queue est donc composée de (460, 12, 23).
La liste complète est donc (1, 460, 12, 23).
03° Sans l'information couleur. Quel élément forme ici la tête ? Quelle est la séquence qui forme la queue ? Que contient au total la liste ?
21 → 12 → 13 → 0
...CORRECTION...
La tête est ici identifiée par le sens des flèches : c'est le premier élément.
La tête contient donc 21.
La queue est donc composée de (12, 13, 0).
La liste complète est donc (21, 12, 13, 0).
04° Quel élément forme ici la tête ? Quelle est la séquence qui forme la queue ? Que contient au total la Liste ?
20 ← 45 ← 10 ← 18
...CORRECTION...
La tête est ici identifiée par le sens des flèches : c'est le premier élément.
La tête contient donc 18.
La queue est donc composée de (10, 45, 20).
La liste complète est donc (18, 10, 45, 20).
05° Seule la tête est indiquée. Quel élément forme ici la tête ? Quelle est la séquence qui forme la queue ? Que contient au total la Liste ?
23 - 12 - 460 - 1
...CORRECTION...
La tête est ici identifiée par la couleur.
La tête contient donc 1.
La queue est donc composée des éléments situés linéairement derrière cette tête : (460, 12, 23).
La liste complète est donc (1, 460, 12, 23).
2) Représentations du contenu d'une Liste
Comment représenter une telle Liste ?
2a) Représentation Tête - Queue
Une tête menant à une queue, voilà ce qui est vraiment fondamental dans une Liste.
5 → 8 → 2 → 3
Le 5 étant la tête de la Liste qu'on nommera lst1, on peut noter sa queue lst2.
5 → lst2
On pourrait alors noter ceci : lst1 = (5, lst2).
Et que contient lst2 : une tête 8 et une queue lst3...
8 → lst3
lst2 = (8, lst3)
On obtient alors l'enchaînement suivant (si vous avez déjà fait la partie sur la récursivité, cela devrait vous rappeler l'empilement) :
- lst1 = (5, lst2)
- lst2 = (8, lst3)
- lst3 = (2, lst4)
- lst4 = (3, lst5)
- lst5 = ()
2b) Définition
On remarque donc qu'une Liste peut être
- soit un couple (tête, queue), la tête étant du type abstrait Elément et la queue étant du type abstrait Liste,
- soit l'ensemble vide.
On pourrait remonter dans l'autre sens dans nos déclarations et obtenir ceci :
- lst4 = (3, ())
- lst3 = (2, (3, ()))
- lst2 = (8, (2, (3, ())))
- lst1 = (5, (8, (2, (3, ()))))
Remarquez bien que la queue de lst4 est vide. C'est possible puisque qu'une queue est une liste et qu'une liste peut être vide.
2c) Représentation en séquence ordonnée
On dispose donc de pluqsieurs façons pour représenter symboliquement nos listes :
Avec des parenthèses : (5, (8, (2, (3)))) ou plus facilement par (5, 8, 2, 3)
Avec des crochets : [5, [8, [2, [3]]]] ou plus facilement par [5, 8, 2, 3]
Avec des accolades : {5, {8, {2, {3}}}} ou plus facilement par {5, 8, 2, 3}
Attention, avec cette notation, à ne pas confondre avec les vrais ensembles mathématiques où un élément ne peut être présent qu'une fois.
Ou avec chevrons : <5, <8, <2, <3>>>> ou plus facilement par <5, 8, 2, 3>
Il faut juste choisir, le noter clairement.
Ici, nous utiliserons des parenthèses par exemple.
La représentation n'est qu'une apparence externe
Comprennez bien qu'on peut représenter des données identiques de plusieurs façons, tout en ne changeant rien aux données elles-mêmes.
C'est le principe de l'interface : la mécanique interne de fonctionnement est indépendante de la façon dont on génère sa représentation interne.
Lorsqu'on décide de dire qu'on va écrire les listes en utilisant les parenthèses ou les crochets ou les accolades, cela ne veut pas dire qu'à l'interne ce sont des n-uplets, des tableaux ou des dictionnaires.
06° Donner deux représentations de la liste suivante (en mode (tete, queue)) puis comme une simple séquence linéaire d'éléments :
12 → 4
...CORRECTION...
En représentation (tête, queue)
(12, liste2)
(12, (4, ()))
En séquence linéaire : (12, 4)
07° Donner deux représentations de la liste suivante (en mode (tete, queue)) puis comme une simple séquence linéaire d'éléments :
5 → 2 → 10
...CORRECTION...
Première représentation
(5, liste2)
(5, (2, liste3))
(5, (2, (10, ())))
La deuxième représentation est donc (5, 2, 10).
3) Définition compléte du type abstrait Liste
On peut donner une définition avec des PRECONDITIONS et des POSTCONDITIONS.
- listeVide() → Liste
- estListeVide(lst:Liste) → Booléen
- insérer(lst:Liste, elt:Elément, i:Entier Naturel) → Liste
- supprimer(lst:Liste, i:Entier Naturel) → Liste
- acceder(lst:Liste, i:Entier Naturel) → Zone de stockage
- lire(ref:Zone de stockage) → Elément
- successeur(ref:Zone de stockage) → Zone de stockage
- longueur(lst:Liste) → Entier Naturel
POSTCONDITION : Renvoie la référence d'une nouvelle Liste qui est vide initialement.
POSTCONDITION : Renvoie VRAI si la liste lst fournie est vide, FAUX sinon.
PRECONDITIONS : l'indice i caractérise un indice valide permettant de localiser une position, et l'élément elt doit avoir un type compatible avec ce type de liste.
POSTCONDITION : Renvoie une nouvelle Liste comportant le nouvel élément dont la position dépend de l'Identifiant fourni (avant, après..., c'est à définir clairement dans la documentation, mais rien n'est imposé : il existe donc beaucoup de variantes valides).
PRECONDITION : l'indice est un indice valide.
POSTCONDITION : Renvoie une nouvelle liste dans laquelle l'identifiant désigné a été supprimé.
PRECONDITION : l'indice i caractérise un indice valide (compris entre 0 et la longueur -1 si on commence la numérotation à 0).
POSTCONDITION : Renvoie l'identifiant de l'élément correspond à l'indice fourni.
PRECONDITION : ref caractérise la référence d'une zone valide.
POSTCONDITION : Renvoie l'élément stocké à l'identifiant envoyé.
PRECONDITION : ref caractérise la référence d'une zone valide.
POSTCONDITION : Renvoie l'identifiant de l'élément qui suit. S'il n'y en a plus, il faut renvoyer un identifiant signalant qu'il n'y a pas de successeur (à définir)
POSTCONDITION : Renvoie le nombre d'éléments stockés dans la liste.
L'une des spécificités du type abstrait Liste est que sa définition est plutôt large. Il n'existe pas réellement de normalisation des fonctions d'interface par exemple.
Le tout est que votre propre version possède bien des primitives du type Liste.
Toutes les structures de données qui collent à la définition et qui possèdent des fonctions d'interface répondant à ces critères sont donc des listes.
2 - Définitions précises
Exemple 1 : Interface plutôt restrictive qui n'agit que sur la tête
Pour ce premier exemple, on travaillera avec un type abstrait immuable.
Cette proposition mime les listes de LISP initialement : les primitives sont toutes liées à des actions sur la tête. On se donne le droit d'aller lire tous les éléments qu'on veut mais on ne peut agir directement que sur la tête d'une Liste.
A chaque fois qu 'on doit fournir un indice, on considère donc qu'il vaut 0 et il est donc inutile de l'envoyer.. Les fonctions ayant un indice à fournir en paramètre ne demandent donc pas à recevoir quelque chose pour ce paramètre : sa valeur par défaut est 0.
Voici les prototypes et signatures des fonctions d'interface :
- listeVide() → Liste
- estListeVide(lst:Liste) → Booléen
- insererEnTete(lst:Liste, elt:Elément) → Liste
- supprimerTete(lst:Liste) → Liste
- acceder(lst:Liste, i:Entier Naturel) → Zone de stockage
- lire(ref:Zone de stockage) → Elément
- successeur(ref:Zone de stockage) → Zone de stockage
- longueur(lst:Liste) → Entier Naturel
POSTCONDITION : Renvoie la référence d'une nouvelle Liste qui est vide initialement.
Exemple d'utilisation
lstA = listeVide()
Le contenu de lstA est alors () par exemple.
POSTCONDITION : Renvoie VRAI si la liste lst fournie est vide, FAUX sinon.
Exemple d'utilisation
estListeVide(lstA) renvoie alors VRAI.
PRECONDITIONS : elt doit avoir un type compatible avec ce type de liste.
POSTCONDITION : Renvoie une nouvelle Liste dont elt est l'élément de Tête et dont la queue est la Liste lst précédente.
La Liste est ici immuable puisqu'on renvoie une nouvelle Liste, plutôt que de juste modifier l'ancienne en mémoire.
Historiquement, dans LISP cette fonction se nomme cons (comme _cons_truct).
Exemple d'utilisation
lstA = listeVide()
lstB = insererEnTete(5, lstA)
lstB contient alors (5, ()) qu'on pourrait noter simplement (5,).
lstB = insererEnTete(15, lstB)
lstB contient alors quelque chose comme (15, (5, ())), qu'on peut plutôt représenter par (15, 5).
PRECONDITION : la Liste lst ne doit pas être vide.
POSTCONDITION : Renvoie la queue de lst.
Historiquement, dans LISP cette fonction se nomme cdr (contents of decrement register).
Exemple d'utilisation
On considère que lstB contient (25, (15, (5, ()))) ou (25, 15, 5)
lstC = supprimerTete(lstB)
lstC contiendra alors (15, (5, ())) ou (15, 5).
lstB contient toujours (25, (15, (5, ())))
PRECONDITION : l'indice i caractérise un indice valide (compris entre 0 et la longueur -1 si on commence la numérotation à 0).
POSTCONDITION : Renvoie l'identifiant de l'élément correspond à l'indice fourni.
On trouve un cas particuler : accéder à la Tête qui est alors définie comme l'indice 0.
tete(lst:Liste) → Zone de stockage
PRECONDITION : La liste lst ne doit pas être vide.
POSTCONDITION : Renvoie l'identifiant de la zone de Tête.
PRECONDITION : ref caractérise la référence d'une zone valide.
POSTCONDITION : Renvoie l'élément stocké à l'identifiant envoyé.
Exemple d'utilisation
On considère que lstB contient (25, (15, (5, ())))
ref = tete(lstB)
recup = lire(ref)
recup contient alors 25. La liste lstB n'a pas été modifiée.
On aurait pu noter directement :
recup = lire(tete(lstB))
On aurait également pu noter :
recup = lire(acceder(lstB, 0))
On trouvera souvent également une fonction "raccourci" facilement réalisable en combinant lire() et tete() qui permet d'obtenir directement le premier élément de la Liste :
premier(lst:Liste) → Elément
PRECONDITION : lst est une Liste non vide.
POSTCONDITION : Renvoie l'élément stocké en tête.
Exemple d'utilisation
On considère que lstB contient (25, (15, (5, ())))
recup = premier(lstB)
recup contient alors 25. La liste lstB n'a pas été modifiée.
PRECONDITION : l'identifiant caractérise un identifiant valide.
POSTCONDITION : Renvoie l'identifiant de l'élément qui suit.
Exemple d'utilisation
On considère que lstB contient (25, (15, (5, ())))
ref = tete(lstB)
suivant = successeur(ref)
suivant = successeur(suivant)
recup = lire(suivant)
On obtient alors la valeur 5 dans recup. La liste lstB n'a pas été modifiée.
POSTCONDITION : Renvoie le nombre d'éléments stockés dans la liste.
Exemple d'utilisation
On considère que lstB contient (25, (15, (5, ())))
nb = longueur(lstB)
On obtient alors la valeur 3 dans nb.
Si on résume :
- listeVide() → Liste
- estListeVide(lst:Liste) → Booléen
- insererEnTete(lst:Liste, elt:Elément) → Liste
- supprimerTete(lst:Liste) → Liste
- acceder(lst:Liste, i:Entier Naturel) → Zone de stockage
- tete(lst:Liste) → Zone de stockage
- lire(ref:Zone de stockage) → Elément
- premier(lst:Liste) → Elément
- successeur(ref:Zone de stockage) → Zone de stockage
- longueur(lst:Liste) → Entier Naturel
On notera que plusieurs fonctions ci-dessous auraient pu être omises puisqu'on peut les recréer à partir des autres. Mais s'agissant d'opérations courantes sur les Listes, on a tendance à les rajouter plutôt qu'à les refaire.
08° Donner le contenu des variables au fur et à mesure de l'exécution de ce code. J'utilise une syntaxe Python pour mimer un pseudo-langage.
1
2
3
4
5
6 | |
...CORRECTION...
Ligne 1 : lstA contient (4, ()) ou (4,)
Ligne 2 : lstB contient (6, (4, ())) ou (6, 4)
Ligne 3 : lstC contient (0, (6, (4, ()))) ou (0, 6, 4)
Ligne 4 : x contient 0
Ligne 5 : lstD contient (6, (4, ())) ou (6, 4)
Ligne 6 : on récupère la zone de tête, on cherche son successeur et on lit l'élément qui s'y trouve : c'est donc 4.
Bon, maintenant que vous avez compris le principe de la tête et de la queue, nous allons représenter de cette façon simplifiée la liste tant qu'elle ne comporte que des éléments de même type :
lstC contient (0, (6, (4, ())))
lstC représentée par (0, 6, 4)
Tiré de Wikipédia :
Cette utilisation des parenthèses pour générer des listes dans LISP donne lieu à des moqueries utilisant l'acronyme LISP : « Lots of Irritating and Silly Parentheses »
(« Des tas de parenthèses irritantes et idiotes »), ou « Lots of Insipid and Stupid Parentheses »
(« Des tas de parenthèses insipides et stupides »), ou « Langage Informatique Stupidement Parenthésé »
, ou « Langage Insipide Saturé de Parenthèses »
.
09° Fournir l'ensemble des instructions qui vont permettre de passer de la liste lstA contenant initialement (0, 6, 4) à un contenu correspondant à (10, 6, 4)
Voici la première ligne en pseudo-Python pour vous éviter de la taper :
1 | |
Sur copie papier, on se permettra un alias insT() pour la fonction insererEnTete().
1 | |
...CORRECTION...
1
2
3 | |
10° Fournir l'ensemble des instructions qui vont permettre de passer de la liste lstA contenant initialement (0, 6, 4) à un contenu correspondant à (10, 45, 4)
Voici le début en pseudo-Python si ça peut vous éviter de la taper :
1 | |
...CORRECTION...
1
2
3
4
5 | |
Ou alors en moins long mais avec de l'imbrication :
1
2
3 | |
Si vous avez déjà fait l'activité Récursivité, vous devriez voir qu'on va pouvoir utiliser la récursivité pour réaliser ces changements.
Avec les opérations de base (création, suppression, rajout, lecture) de la tête, on peut finalement agir comme on le veut, partout dans la liste. Par contre, cela aura un coût, nous en parlerons justement en TP.
Certaines implémentations seront meilleures que d'autres en fonction des opérations réalisées couramment.
C'est l'une des raisons de la difficulté à définir précisement ce type abstrait Liste : chacun aura son assemblage préféré de fonctions d'interface.
Elles auront toutes les mêmes possibilités théoriques mais pas toutes la même efficacité sur certaines tâches.
Exemple 2 : Liste plus souple avec accès direct aux éléments numérotés
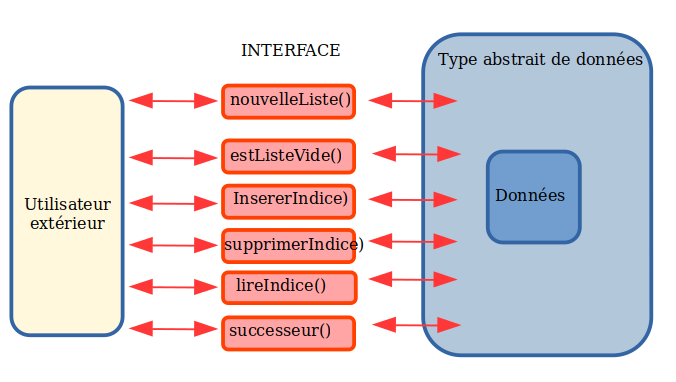
- listeVide() -> Liste
Crée une nouvelle liste vide (). - estListeVide(lst:lst) -> bool
Renvoie un booléen qui vaut True si la liste lst transmise est une liste vide. - insererEnIndice(x:Elt, lst:Liste, i:int) -> Liste
Renvoie une nouvelle liste où l'élément fourni x est maintenant l'élément de la liste situé à l'indice i. On prendra ici un système de position lié à un indice commençant à 0. - supprimerIndice(lst:Liste, i:int) -> Liste
Renvoie une nouvelle liste où l'élément à l'indice i est supprimé, rendant la liste moins longue. - lireIndice(lst:lst, i:int) -> Liste
Renvoie l'élément stocké à l'indice i.
Cette fois, l'identifiant est simplement le numéro d'indice.
Exemple d'utilisation
lstA = listeVide()
Le contenu de lstA est ().
Exemple d'utilisation
lstA = listeVide()
estListeVide(lstA) va donc renvoyer True
Exemple d'utilisation
lstA = (12, 15, 18, 4)
lstB = insererIndice(5, lstA, 2)
lstB contient alors (12, 15, 5, 18, 4).
lstA = (12, 15, 18, 4)
lstB = supprimerIndice(lstA, 1)
lstB contient alors (12, 18, 4).
Exemple d'utilisation
lstA = (12, 15, 18, 4)
reponse = lirePosition(lstA, 1)
reponse contient alors 15.
Si vous regarder bien cette liste, vous pourrez voir qu'on retrouve ce qu'on est capable de faire avec des tableaux.
3 - Implémentation
Lorsqu'on veut réellement réaliser un programme, il faut passer de l'abstraction algorithmique (un algorithme agissant sur des types abstraits) à une réalisation pratique (programme agissant sur des structures de données).
Implémentation et encapsulation
En informatique, l'implémentation est le passage de l'abstraction théorique à la programmation concrète.
Vous avez déjà implémenté des algorithmes en programmes Python ou Javascript.
Vous allez maintenant implémenter un type abstrait en structure de données réelles en machine.
L'utilisateur n'a à connaître que les rôles et prototypes des fonctions d'interface. Deux avantages :
- Si vous désirez modifier le code interne de la structure de données pour qu'elle soit plus performante, rien ne change de l'extérieur : les programmes de l'utilisateur seront toujours fonctionnels.
- La structure de données a été concue et vérifiée pour être fonctionnelle. L'utilisateur n'a pas à modifier ce code au risque de le casser, parfois sans s'en rendre compte.
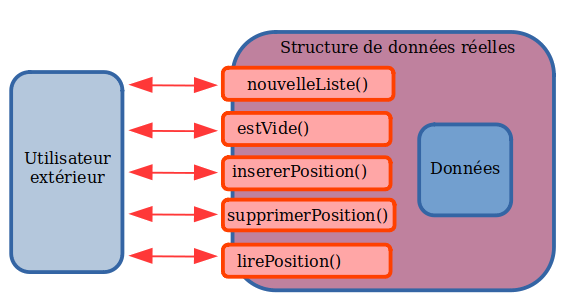
C'est le principe de l'encapsulation, que nous avons déjà rencontré également sur les objets. Ce principe peut bien entendu être utilisé sur des programmes non-objet.
Selon les langages, certains types abstraits sont déjà implémentés efficacement en pratique. Le langage de programmation possède alors déjà des classes ou des types natifs permettant de les utiliser.
Par exemple, en Python :
- On gère le type abstrait booléen en utilisant le type concret natif bool.
- On gère le type abstrait integer en utilisant le type concret natif int.
- On gère le type abstrait nombre à virgule flottante en utilisant le type concret natif float.
- On gère le type abstrait tableau statique (array en anglais) en utilisant le type concret natif ... list.
- On gère le type abstrait tableau dynamique (vector en anglais) en utilisant le type concret natif list.
- On gère le type abstrait tableau associatif en utilisant le type concret natif dict.
- On gère le type abstrait p-uplet nommé en utilisant le type concret natif dict.
- On gère le type abstrait p-uplet en utilisant le type concret natif tuple.
Comme vous le voyez, certains noms vont à la fois référence à un type abstrait et à une structure de données présente nativement dans un langage.
Nous allons voir la prochaine fois qu'il y a globalement trois façons de voir les listes :
Implémentations courantes
On implémente souvent les listes sous trois formes :
- La forme p-uplet (tête, queue) : on retrouve alors une structure de données proches de celles des piles. On a une implémentation facile à comprendre mais
- la lecture et la modification sont à coût linéaire dans le pire des cas
- le rajout et la suppression est à coût linéaire dans le pire des cas
- la concaténation de deux listes à coût linéaire.
- Nous avions l'exemple suivant : 5 → 8 → 2 → 3 qui peut donc être vu comme des couples tête-queue imbriqués les uns dans les autres :
- Cette structure de données est souvent basée sur des tuples de deux éléments : la tête et la queue
- La forme liste contiguë : on utilise un tableau statique où les "cases" sont réellement les unes derrière les autres en mémoire. Si l'implémentation en machine est de bien réalisée :
- la lecture et la modification sont à coût constant dans le pire des cas
- le rajout et la suppression est à coût linéaire dans le pire des cas
- la concaténation de deux listes à coût linéaire
- Nous avions l'exemple suivant : 5 → 8 → 2 → 3 qui peut donc être vu comme les cases d'un tableau statique :
- Cette structure de données est souvent basée sur des tableaux dont les éléments sont ceux de la lise.
- La forme liste chaînée : on utilise une succesion de cellules qui contiennent la référence de la cellule suivante.
Activité publiée le 21 09 2020
Dernière modification : 25 09 2022
Auteur : ows. h.
Modification : Andjekel