Un parcours d'arbre est une façon d'ordonner les nœuds d'un arbre afin de les parcourir. On peut le voir comme une fonction qui à un arbre associe une liste de ses nœuds même si la liste n'est souvent pas explicitement construite par le parcours.

On distingue essentiellement deux types de parcours : le parcours en largeur et les parcours en profondeur. Parmi les parcours en profondeur, on distingue à nouveau le parcours préfixe, le parcours infixe et le parcours suffixe.

 

 

Parcours en profondeurs

Les parcours en profondeur se définissent de manière récursive sur les arbres. Le parcours d'un arbre consiste à traiter la racine de l'arbre et à parcourir récursivement les sous-arbres gauche et droit de la racine. Les parcours préfixe, infixe et suffixe se distinguent par l'ordre dans lequel sont faits ces traitements.

Définitions et exemples

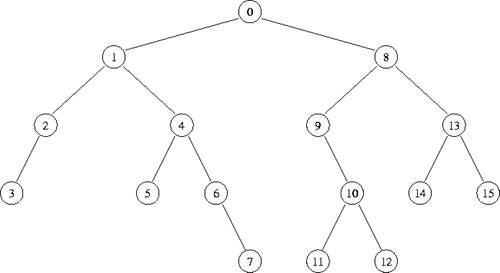
Dans le parcours préfixe, la racine est traitée avant les appels récursifs sur les sous-arbres gauche et droit (faits dans cet ordre). Le parcours préfixe de l'arbre ci-dessus parcourt les nœuds dans l'ordre [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15].

Dans le parcours infixe, le traitement de la racine est fait entre les appels sur les sous-arbres gauche et droit. Le parcours infixe de l'arbre ci-dessus parcourt les nœuds dans l'ordre [3,2,1,5,4,6,7,0,9,11,10,12,8,14,13,15].

Dans le parcours suffixe, la racine est traitée après les appels récursifs sur les sous-arbres gauche et droit (faits dans cet ordre). Le parcours suffixe de l'arbre ci-dessus parcourt les nœuds dans l'ordre [3,2,5,7,6,4,1,11,12,10,9,14,15,13,8,0].

 

 

 

 

Parcours en largeur

Définition et exemple

Le parcours en largeur consiste à parcourir l'arbre niveau par niveau. Les nœuds de niveau 0 sont d’abord parcourus puis les nœuds de niveau 1 et ainsi de suite. Dans chaque niveau, les nœuds sont parcourus de la gauche vers la droite. Le parcours en largeur de l'arbre ci-dessus parcours les nœuds dans l'ordre [0,1,8,2,4,9,13,3,5,6,10,14,15,7,11,12].