Algorithme sur les Arbres binaires

1) notations utilisées

Dans ce chapitre nous allons utiliser les notations suivantes :

Soit un arbre T : T.racine correspond au noeud racine de l'arbre T

Soit un noeud x :

x.gauche correspond au sous-arbre gauche du noeud x
x.droit correspond au sous-arbre droit du noeud x
x.clé correspond à la clé du noeud x

Il faut noter que si le noeud x est une feuille, x.gauche et x.droite sont des arbres vides (NIL)

2) calculer la hauteur d'un arbre

Voici l'algorithme qui permet de calculer la hauteur d'un arbre :

VARIABLE
T : arbre
x : noeud

DEBUT
HAUTEUR(T) :
  si T ≠ NIL :
    x ← T.racine
    renvoyer 1 + max(HAUTEUR(x.gauche), HAUTEUR(x.droit))
  sinon :
    renvoyer 0
  fin si
FIN

N.B. la fonction max renvoie la plus grande valeur des 2 valeurs passées en paramètre (exemple : max(5,6) renvoie 6

Nous avons ici un algorithme récursif. Vous aurez l'occasion de constater que c'est souvent le cas dans les algorithmes qui travaillent sur des structures de données telles que les arbres.

3) calculer la taille d'un arbre

Nous allons maintenant étudier un algorithme qui permet de calculer le nombre de noeuds présents dans un arbre.

VARIABLE
T : arbre
x : noeud

DEBUT
TAILLE(T) :
  si T ≠ NIL :
    x ← T.racine
    renvoyer 1 + TAILLE(x.gauche) + TAILLE(x.droit)
  sinon :
    renvoyer 0
  fin si
FIN

4) parcours d'un arbre

a) introduction

Il existe plusieurs façons de parcourir un arbre (parcourir un arbre = passer par tous les noeuds), nous allons en étudier quelques-unes. Le choix du parcours dépend du problème à traiter

Vous trouverez sur le lien ci-contre trois DEFINITIONS

b) parcourir un arbre dans l'ordre préfixe

Le parcours préfixe est un parcours en profondeur d'abord.

Méthode du parcours préfixe

(parfois aussi appelé préordre)

Chaque nœud est visité avant que ses fils le soient.

On part de la racine, puis on visite son fils gauche (et éventuellement le fils gauche de celui-ci, etc.) avant de remonter et de redescendre vers le fils droit.

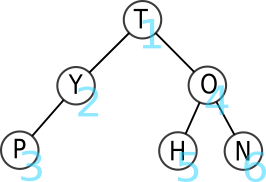
L'ordre des lettres parcourues est donc T-Y-P-O-H-N.
Comme vous pouvez le constater ci-dessus, dans le cas du parcours préfixe, on affiche chaque noeud avant de parcourir son sous-arbre gauche et son sous-arbre droit.

Voici l'algorithme qui va permettre de parcourir un arbre dans l'ordre préfixe :

VARIABLE
T : arbre
x : noeud

DEBUT
PARCOURS-PREFIXE(T) :
  si T ≠ NIL :
    x ← T.racine
    affiche x.clé
    PARCOURS-PREFIXE(x.gauche)
    PARCOURS-PREFIXE(x.droit)
  fin si
FIN

c) parcourir un arbre dans l'ordre suffixe

Le parcours suffixe est aussi un parcours en profondeur d'abord.

Méthode du parcours suffixe

(parfois aussi appelé post-ordre ou encore postfixe)

Chaque nœud est visité après ses fils le soient.

On part donc de la feuille la plus à gauche, et on ne remonte à un nœud père que si ses fils ont tous été visités.

L'ordre des lettres parcourues est donc P-Y-H-N-O-T.

Dans le cas du parcours suffixe, on affiche chaque noeud après avoir parcouru son sous-arbre gauche et son sous-arbre droit.

Voici l'algorithme qui va permettre de parcourir un arbre dans l'ordre suffixe :

VARIABLE
T : arbre
x : noeud

DEBUT
PARCOURS-SUFFIXE(T) :
  si T ≠ NIL :
    x ← T.racine
    PARCOURS-SUFFIXE(x.gauche)
    PARCOURS-SUFFIXE(x.droit)
    affiche x.clé
  fin si
FIN

d) parcourir un arbre dans l'ordre infixe

Le parcours infixe est aussi un parcours en profondeur d'abord.

Méthode du parcours infixe

(parfois aussi appelé en ordre)

Chaque nœud est visité après son fils gauche mais avant son fils droit.

On part donc de la feuille la plus à gauche et on remonte par vagues sucessives. Un nœud ne peut pas être visité si son fils gauche ne l'a pas été.

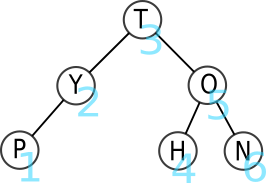
L'ordre des lettres parcourues est donc P-Y-T-H-O-N.

Dans le cas du parcours infixe, pour un noeud A donné, on parcourra le sous-arbre gauche de A, puis on affichera la clé de A puis enfin, on parcourra le sous-arbre droite de A

Voici l'algorithme qui va permettre de parcourir un arbre dans l'ordre infixe :

VARIABLE
T : arbre
x : noeud

DEBUT
PARCOURS-INFIXE(T) :
  si T ≠ NIL :
    x ← T.racine
    PARCOURS-INFIXE(x.gauche)
    affiche x.clé
    PARCOURS-INFIXE(x.droit)
  fin si
FIN

Comment ne pas se mélanger entre le pré / in / post fixe ?

pré veut dire avant
in veut dire au milieu
post veut dire après

Ces trois mots-clés parlent de la place du père par rapport à ses fils. Ensuite, il faut toujours se souvenir qu'on traite le fils gauche avant le fils droit.

préfixe : le père doit être le premier par rapport à ses fils.
infixe : le père doit être entre son fils gauche (traité en premier) et son fils droit.
postfixe : le père ne doit être traité que quand ses deux fils (gauche d'abord, droite ensuite) l'ont été.

Un parcours préfixe commencera toujours par la racine, alors qu'un parcours postfixe finira toujours par la racine. Dans un parcours infixe, la racine sera «au milieu» (pas nécessairement parfaitement).

e) parcourir un arbre en largeur d'abord

BFS : Breadth First Search

Méthode du parcours en largeur (BFS)

Le parcours en largeur d'abord est un parcours étage par étage (de haut en bas) et de gauche à droite.

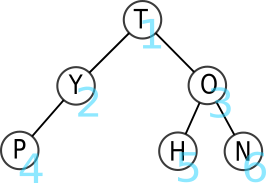
L'ordre des lettres parcourues est donc T-Y-O-P-H-N.

Dans le cas d'un parcours en largeur d'abord on affiche tous les noeuds situés à une profondeur n avant de commencer à afficher les noeuds situés à une profondeur n+1.

Voici l'algorithme qui va permettre de parcourir un arbre en largeur d'abord :

T : arbre
Tg : arbre
Td : arbre
x : noeud
f : file (initialement vide)

DEBUT
PARCOURS-LARGEUR(T) :
  enfiler(T.racine, f) //on place la racine dans la file
  tant que f non vide :
    x ← defiler(f)
    affiche x.clé
    si x.gauche ≠ NIL :
      Tg ← x.gauche
      enfiler(Tg.racine, f)
    fin si
    si x.droit ≠ NIL :
      Td ← x.droite
      enfiler(Td.racine, f)
    fin si
  fin tant que
FIN

Vous noterez aussi que cet algorithme n'utilise pas de fonction récursive. Il est aussi important de bien noter l'utilisation d'une file (FIFO) pour cet algorithme de parcours en largeur.

5) Applications

activité 1

Soit l'arbre suivant :

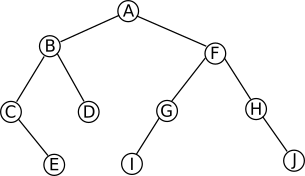
Appliquez l'algorithme qui permet de calculer le hauteur d'un arbre binaire à l'arbre ci-dessus. Quel résultat obtenez-vous ?

activité 2

Soit l'arbre suivant :

Appliquez l'algorithme qui permet de calculer la taille d'un arbre binaire à l'arbre ci-dessus. Quel résultat obtenez-vous ?

activité 3

ÉnoncéCorr. largeurCorr. préfixeCorr. infixeCorr. postfixe

Donner le rendu de chaque parcours :

Parcours en largeur
Parcours préfixe
Parcours infixe
Parcours postfixe

largeur : 1 2 3 4 5 6 7 8 9

préfixe : 1 2 4 5 7 8 3 6 9

infixe : 4 2 7 5 8 1 3 9 6

postfixe : 4 7 8 5 2 9 6 3 1

activité 4

ÉnoncéCorr. largeurCorr. préfixeCorr. infixeCorr. postfixe

Donner le rendu de chaque parcours :

Parcours en largeur
Parcours préfixe
Parcours infixe
Parcours postfixe

largeur : 9 8 7 6 2 5 1 4 3

préfixe : 9 8 6 2 1 7 5 4 3

infixe : 6 8 1 2 9 7 4 5 3

postfixe : 6 1 2 8 4 3 5 7 9