Autre exemple de recherche dichotomique

⏬

Principe

Principe de la recherche dichotomique - Exemple de 70 dans la liste

Si les tableaux s'affichent sans couleur ou si les animations semblent ne pas fonctionner, il faut que vous relanciez la page à jour de façon à mettre vos fichiers CSS à jour.

Dans le tableau trié de la question a.

On a 20 éléments d'index compris entre 1 et 20 et de valeurs :

6, 8, 9, 13, 18, 37, 37, 59, 60, 60, 61, 68, 70, 80, 80, 83, 83, 89, 91, 96

Sous forme d'un tableau :

	↦																			↤
Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Elément	6	8	9	13	18	37	37	59	60	60	61	68	70	80	80	83	83	89	91	96

b. Cherchons si 70 est présent dans ce tableau.

En recherche séquentielle, on regarderait l'index 1 (6) à l'index 13 (70)... Ici, il faut donc 13 boucles et 13 comparaisons.

Utlisons la recherche dichotomique.

Etape 1 - Intervalle de départ [1 ; 20]

on considère un point gauche d'index 1 : gauche = 1.
on considère un point droite d'index 20 : droite = 20.
On calcule l'index central ou milieu à l'aide d'un division entière : (1+20)//2 donne 10 On aura donc milieu = 10.


Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Elément	6	8	9	13	18	37	37	59	60	60	61	68	70	80	80	83	83	89	91	96

Comme tableau[10] = 60 et qu'on cherche 70 dans un tableau trié, on ne garde que la partie à droite du point central d'index 10.

On va alors changer le point droit avec gauche = 11

On recommence ces opérations sur le nouvel intervalle [11 ; 20].

Etape 2 : Intervalle [11 ; 20]

on considère un point gauche d'index 11 : gauche = 11.
on considère un point droite d'index 20 : droite = 20.
On calcule l'index central ou milieu à l'aide d'un division entière : (11+20)//2 donne 15 On aura donc milieu = 15.


Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Elément	6	8	9	13	18	37	37	59	60	60	61	68	70	80	80	83	83	89	91	96

Comme l'index 15 fait référence à 80 et qu'on cherche 70 dans un tableau trié, on ne garde que la partie à gauche de l'index 15.

On va alors changer le point droit avec droite = 14

On recommence ces opérations sur le nouvel intervalle [11 ; 14].

Etape 3 : Intervalle [11 ; 14]

on considère un point gauche d'index 11 : gauche = 11.
on considère un point droite d'index 14 : droite = 14.
On calcule l'index central ou milieu à l'aide d'un division entière : (11+14)//2 donne 12 On aura donc milieu = 12.


Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Elément	6	8	9	13	18	37	37	59	60	60	61	68	70	80	80	83	83	89	91	96

Comme l'index 12 fait référence à 68 et qu'on cherche 70 dans un tableau trié, on ne garde que la partie à droite de l'index 12.

On va alors changer le point gauche avec gauche = 13

On recommence ces opérations sur l'intervalle [13 ; 14].

Etape 4 : Intervalle [13 ; 14]

on considère un point gauche d'index 13 : gauche = 13.
on considère un point droite d'index 14 : droite = 14.
On calcule l'index central ou milieu à l'aide d'un division entière : (13+14)//2 donne 13 On aura donc milieu = 13.


Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Elément	6	8	9	13	18	37	37	59	60	60	61	68	70	80	80	83	83	89	91	96

Comme l'index 13 fait référence à 70 et qu'on cherche 70.

Conclusion : 70 appartient à notre tableau.

Réponse obtenue avec 4 comparaisons.

Pour résumer

Si vous voulez revoir la progression de la recherche, voici l'animation globale.


Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Elément	6	8	9	13	18	37	37	59	60	60	61	68	70	80	80	83	83	89	91	96

On peut aussi possible de représenter le principe de l'algorithme de recherche dichotomique avec le schéma suivant:

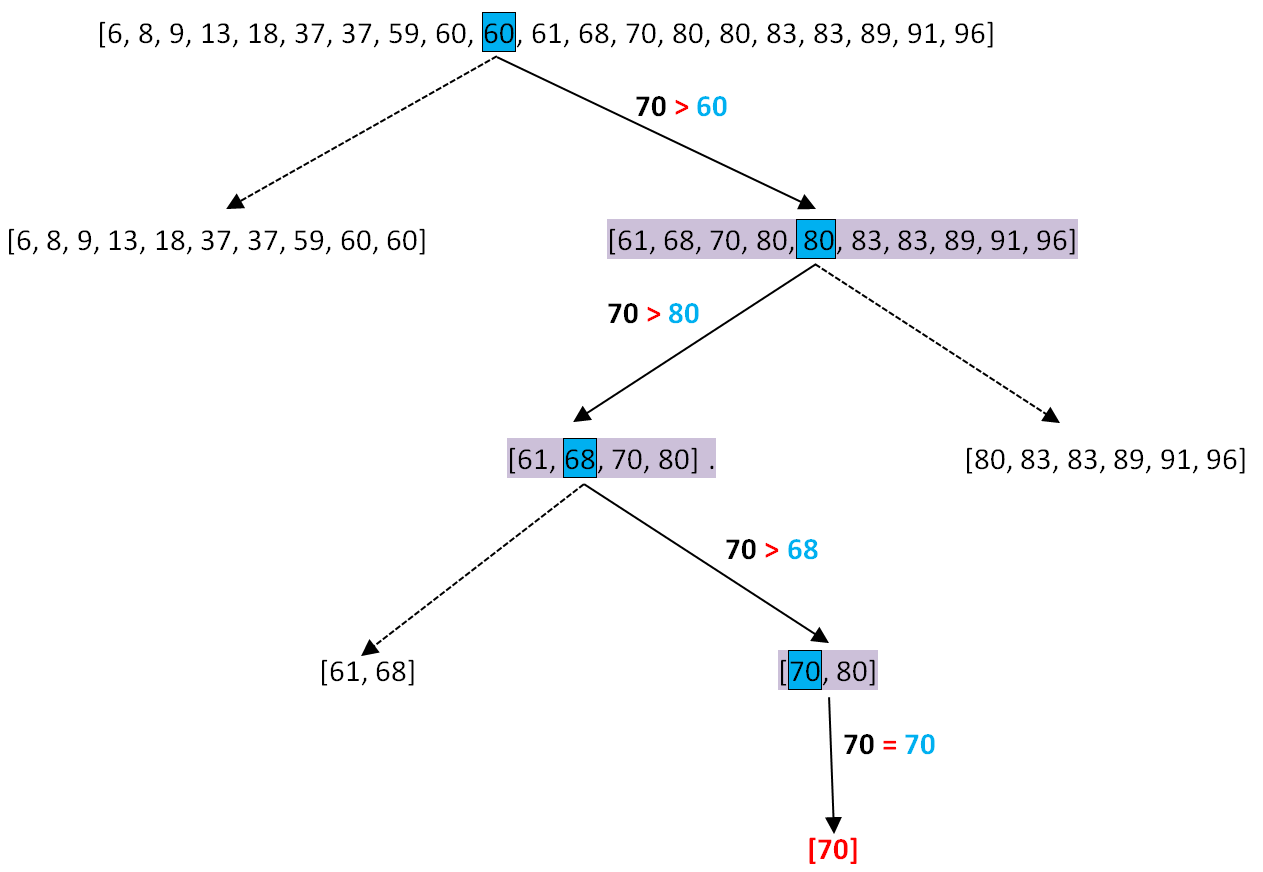
La liste finale contient 70 , donc 70 est dans la liste.

Activité publiée le 21 04 2020
Dernière modification : 12 04 2021
Auteurs : ows. h. et modifié par Andjekel

⏫

Retour au cours

⏪