Parcours séquentiel d'un tableau
Nous allons maintenant voir ce qu'est l'algorithmique.
Après avoir vu cette partie en 1er, vous pourrez répondre à ces questions
- A quoi sert l'algorithmique ?
- Comment savoir si un algorithme fonctionne ?
- Comment garantir qu'un algorithme s'arrête ?
- Comment comparer des algorithmes entre eux pour prendre le "meilleur" ?
1 - Algorithme
Définition d'algorithme
Un algorithme est un ensemble fini (au sens dénombrable) d'instructions précises permettant de résoudre une classe de problèmes.
Si l'algorithme ne fonctionne que pour UN cas particulier, on ne parlera pas d'algorithme.
Une manière de calculer 5 x 4 n'est pas un algorithme.
Par contre, une façon de calculer a x b pourrait être vue comme un algorithme.
De façon plus précise, un algorithme fournit une SORTIE en fonction des données fournies en ENTREE.
ENTREE(S) → Algorithme → SORTIE
Gérard Berry parle des algorithmes comme étant des méthodes à appliquer sans réflechir, en suivant machinalement le déroulement et les ordres.
On sépare réflexion et exécution.
La réflexion est utilisée par l'informaticien lors de la création de l'algorithme.
Lors du déroulement, l'ordinateur exécute. Point.
Pourquoi est-il important d'optimiser les algorithmes qu'on utilise maintenant que les machines sont très puissantes ? A cause de l'augmentation énorme du volume de données à traiter.
Vous êtes chef de service. On vous propose de changer l'équipement informatique pour du Tip Top ou d'engager un.e nouvel.le informaticien.ne Tip Top. Quelqu'un qui a pris Informatique dès la 1er. Si si. Alors ? Votre choix ?
Imaginons qu'on veuille identifier quelqu'un dans une base de données comportant n fiches.
Cas 1 : informaticien moyen mais super-ordinateur
- L'algorithme créé par l'informaticien a besoin de
n3opérations pour identifier la personne dans la base de données qui comportenfiches. - L'ordinateur est capable de faire 200 Giga opérations par seconde.
Rappel : 1 G vaut dire 1 Giga soit 1 milliard ou 1.109.
On peut en déduire le temps mis par l'ordinateur pour identifier les personnes en fonction de la taille de la base de données :
t = n**3 / 200E9
01° Calculer les temps mis pour réaliser cette tâche si la base de données possède 5000 fiches (5.103), 5 millions de fiches (5.106), 5 milliards de fiches (5.109).
...CORRECTION...
Pour 5000 fiches :
- En seconde :
N = (5E3)**3 / 200E9 = 0,625 s
Pour 5 millions de fiches :
- En seconde :
N = (5E6)**3 / 200E9 = 625000000 s - En année :
N = (5E6)**3 / (200E9*3600*24*365) = 19.8 ans
Pour 5 milliards de fiches :
- En seconde :
N = (5E9)**3 / 200E9 = 6,25.1017 s - En année :
N = (5E9)**3 / (200E9*3600*24*365) = 19818619990 ans !
Cas 2 : informaticien au top mais ordinateur beaucoup moins performant
- L'algorithme créé par l'informaticien a besoin de
n2opérations pour identifier la personne dans la base de données qui comportenfiches. - L'ordinateur est capable de faire 30 Mega opérations par seconde...
Rappel : 1 M vaut dire 1 Mega soit 1 million ou 1.106.
On peut en déduire le temps mis par l'ordinateur pour identifier les personnes en fonction de la taille de la base de données :
t = n**2 / 30E6
02° Calculer les temps mis pour réaliser cette tâche si la base de données possède 5000 fiches (5.103), 5 millions de fiches (5.106), 5 milliards de fiches (5.109).
...CORRECTION...
Pour 5000 fiches :
- En seconde :
N = (5E3)**2 / 30E6 = 0,83 s
Pour 5 millions de fiches :
- En seconde :
N = (5E6)**2 / 30E6 = 833333 s - En jour :
N = (5E6)**2 / (30E6*3600*24) = 9.6 jours
Pour 5 milliards de fiches :
- En seconde :
N = (5E9)**2 / 30E6 = 833333333333 s - En année :
N = (5E9)**2 / (30E6*3600*24*365) = 26424 ans !
On voit donc bien que l'ordinateur ultra performant n'a en réalité aucun chance face à celui moins performant sur lequel fonctionne un programme efficace.
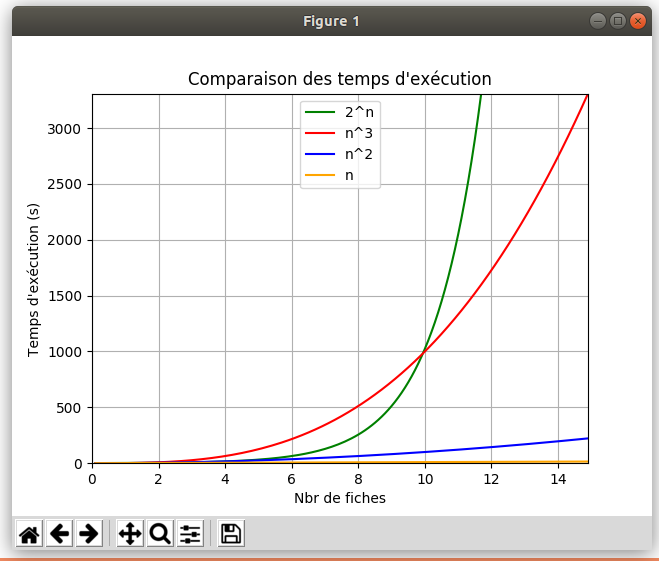
Voici un script Python permettant de générer les courbes ci-dessus.
...PYTHON...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 | # 1 - Importation des modules nécessaires
import math
import matplotlib.pyplot as plt
# 2 - Constantes
# 3 - Déclaration des fonctions
# 4 - Programme principal
# Création des tableaux de données
valeurs_n = [ n for n in range(10000) ] # Abscisse
temps_1 = [ n**3 /200E9 for n in valeurs_n ] # Ordonnée
temps_2 = [ n**2 /30E6 for n in valeurs_n ] # Ordonnée
xmax = max(valeurs_n )
ymax = max(temps_1 )
# Création des courbes
plt.plot(valeurs_n, temps_1, label="Cas 1", color='orange')
plt.plot(valeurs_n, temps_2, label="Cas 2", color='red')
plt.xlabel("Nbr de fiches")
plt.ylabel("Temps d'exécution (s)")
plt.title("Comparaison des temps d'exécution")
plt.legend(loc='upper center')
plt.axis([0, xmax, 0, ymax])
plt.grid()
plt.show() # Affichage à l'écran des courbes
|
Et ça date de quand l'algorithmique ? Des années 2000 ? Des années 1940 ?
Certains pensent que l'un des algorithmes les plus anciens est l'algorithme d'Euclide. Cet algorithme permet de trouver le plus grand diviseur commun (PGDC) de deux entiers a et b. Par exemple, pour a = 15 et b = 20, il s'agit de 5.

Cet algorithme date de -300 et se trouve dans les écrits du mathématicien Euclide d'Alexandrie. Il a été découvert de façon autonome en Inde et en Chine quelques siècles plus tard.
Vers 800, Muhammad Ibn Mūsā al-Khuwārizmī dit Al-Khwarizmi, mathématicien, né dans dans l'actuel Ouzbékistan et mort à Badgad, publie de nombreux textes. Les traductions permettront l'introduction de l'algèbre en Europe. Il a notamment répertorié et classifié de nombreux algorithmes (créés par d'autres). Il y montre leurs terminaisons (le fait qu'ils s'arrêtent bien à tous les coups) ou pas.

Son nom est bien entendu à l'orgine d'algorithme.
Depuis, bien des gens ont travaillé et travaillent toujours pour trouver, créer ou améliorer les algorithmes.
L'un des grands noms de l'algorithmie est Donald Knuth, informaticien et mathématicien américain de renom. Il est un des pionniers de l'algorithmique et a fait de nombreuses contributions dans plusieurs branches de l'informatique théorique (fondements logiques et mathématiques de l'informatique).

Et il reste des choses à découvrir ?
Beaucoup. Il existe notamment une catégorie entière de problèmes dits NP-complets qui posent problème.
L'exemple typique de ce type de problème est le problème du voyageur de commerce : un commercial doit passer par toutes les villes de son secteur. Il cherche à optimer son parcours de façon à ce qu'il prenne le moins de temps possible. Comment trouver la solution optimale ?
Avec 15 villes, on peut énumérer tous les cas possibles et prendre le meilleur. Mais avec 20 000 villes à parcourir, on obtient un temps de calcul beaucoup trop grand pour être exploitable : les tracés routiers risquent d'avoir changé entre temps !
Les propriétés de ces problèmes complexes ?
- Pour un problème donné, vérifier qu'une proposition répond au problème est plutôt rapide et facile avec un programme
- Par contre, le temps de recherche de toutes les solutions possibles pour trouver la solution optimale varie de façon exponentielle avec la taille de l'entrée : cette recherche est donc non exploitable, sauf pour les problèmes aux données d'entrée très réduites.
- Pourtant
- Personne n'a réussi à démontrer qu'il n'existe pas de solution algorithmique plus rapide : il est donc possible qu'une telle solution existe
- On a réussi à démontrer que s'il existe un algorithme efficace sur l'un des problèmes NP-complets, il existe des solutions similaires à tous les autres problèmes NP-complets !
- Souvent une petite modification simplificatrice de l'énoncé du problème le rend immédiatement résolvable en un temps correct...
L'algorithmique est donc un domaine d'études très riche en recherches passées et futures. Si vous aimez les maths, l'informatique et les casses-têtes, c'est un domaine fait pour vous !
2 - Recherche d'un élément dans un tableau
Nous allons maintenant tenter de réaliser un algorithme qui signale si un élément existe dans un tableau (et renvoie son index) ou renvoie une réponse vide sinon.
Cette méthode se nomme également méthode par balayage ou recherche linéaire.
En anglais, on parle de linear search.
Vous allez comprendre tout de suite pourquoi en utilisant l'animation suivante : créer un tableau avec l'un des boutons aléatoires, choisir une valeur à chercher et appuyer sur le bouton lançant l'animation.
Valeur cherchée :
| ↓ | ||||||||||||||||||||
| Indice i | 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Elément | 60 | 89 | 15 | 56 | 82 | 1 | 86 | 97 | 24 | 86 | 75 | 6 | 14 | 69 | 98 | 31 | 37 | 89 | 91 | 56 |
Algorithme de recherche séquentielle
But : trouver si un élément recherché existe bien dans un tableau. S'il existe, on fournit l'index de la première occurence trouvée. Sinon, il renvoie une réponse vide.
Principe : lecture séquentielle et progressive des différents éléments. On renvoie l'index du premier élément qui correspond. VIDE si aucun des éléments n'a correspondu à la recherche.
Description des entrées / sortie
ENTREES:t: un tableau contenant un ensemble d'éléments.x: un élément voulu qu'on tente de rechercher dans le tableau- (optionnelle selon les langages d'implémentation):
longueur, le nombre d'éléments dans le tableau SORTIE: une réponse vide (à définir) ou un nombre correspondant à l'index trouvé.
Exemple :
Prenons t = [13, 18, 89, 1024, 45, -12, 18]
| Indice i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Elément | 13 | 18 | 89 | 1024 | 45 | -12 | 18 |
L'application de l'algorithme de recherche
- sur l'élément 89 doit renvoyer 2 (présence à l'index 2).
- sur l'élément 18 doit renvoyer 1 (présence sur l'index 1 et 6)
- sur l'élement 105 doit renvoyer une valeur signifiant vide (prenons None comme en Python par exemple, ou -1 pour indiquer qu'il s'agit d'une absence d'index).
La valeur exacte de VIDE doit être gérée au moment de l'implémentation dans un langage.
Description de l'algorithme
i ← 0
TANT QUE i < longueur et que t[i] est différent de x
i ← i + 1
Fin TANT QUE
SI i < longueur
Renvoyer i
Fin Si
Renvoyer VIDE
03° Appliquer l'algorithme à la main avec une recherche sur 1024. Vous devriez trouver qu'il renvoie 3. Quelle est la condition qui provoque l'arrêt du TANT QUE : la valeur de la variable index ou le contenu qui correspond à la valeur voulue ?
...CORRECTION...
t ← [13, 18, 89, 1024, 45, -12, 18]
x ← 1024
longueur ← 7
i ← 0
Début du TANT QUE car 0 est inférieur à longueur et t[0] vaut 13 ce qui est différent de 1024
Du coup, i ← 1
Suite du TANT QUE car 1 est inférieur à longueur et t[1] vaut 18 ce qui est différent de 1024
Du coup, i ← 2
Suite du TANT QUE car 2 est inférieur à longueur et t[2] vaut 89 ce qui est différent de 1024
Du coup, i ← 3
Arrêt du TANT QUE car t[3] vaut 1024 !
Evaluation de la condition du SI : i (valant 3) est inférieur à longueur est évaluée à VRAI.
On renvoie 3
04° Appliquer l'algorithme à la main avec une recherche sur 1025. Vous devriez montrer qu'il renvoie VIDE. Quelle est la condition qui provoque l'arrêt du TANT QUE : la valeur de la variable index ou le contenu qui correspond à la valeur voulue ?
...CORRECTION...
t ← [13, 18, 89, 1025, 45, -12, 18]
x ← 1025
longueur ← 7
i ← 0
Début du TANT QUE car 0 est inférieur à longueur et t[0] vaut 13 ce qui est différent de 1025
Du coup, i ← 1
Suite du TANT QUE car 1 est inférieur à longueur et t[1] vaut 18 ce qui est différent de 1025
Du coup, i ← 2
Suite du TANT QUE car 2 est inférieur à longueur et t[2] vaut 89 ce qui est différent de 1025
Du coup, i ← 3
Suite du TANT QUE car 3 est inférieur à longueur et t[3] vaut 89 ce qui est différent de 1025
Du coup, i ← 4
Suite du TANT QUE car 4 est inférieur à longueur et t[4] vaut 45 ce qui est différent de 1025
Du coup, i ← 5
Suite du TANT QUE car 5 est inférieur à longueur et t[5] vaut -12 ce qui est différent de 1025
Du coup, i ← 6
Suite du TANT QUE car 6 est inférieur à longueur et t[6] vaut 18 ce qui est différent de 1025
Du coup, i ← 7
Arrêt du TANT QUE car i vaut 7, ce qui n'est pas inférieur strictement à longueur !
Condition du SI non validée : i (valant 7) inférieur à longueur est évaluée à FAUX.
On renvoie VIDE
05° 18 apparaît deux fois dans le tableau. La valeur renvoyée par cet algorithme sur une recherche sur 18 donne :
- A : 0
- B : 1
- C : 6
- D : (1,6)
Rappel du contenu
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Elément | 13 | 18 | 89 | 1024 | 45 | -12 | 18 |
...CORRECTION...
On lit le contenu progressivement de façon séquentielle.
En lisant l'algorithme, on voit qu'on renvoie la première occurence trouvée, soit 1.
06° Compléter la fonction Python ci-dessous pour qu'elle applique l'algorithme fourni ci-dessus.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | def trouverIndex(t, x):
'''Fonction qui renvoie l'index de l'élément x dans le tableau. None en cas d'échec de la recherche
:: param t(list) :: un tableau contenant le même type d'élément que le paramètre x
:: param x(au choix) :: l'élément qu'on cherche à trouver dans le tableau
:: exemples ::
>>> test = [10,20,30,40,50]
>>> trouverIndex(test, 20)
1
>>> trouverIndex(test, 60)
'''
pass
if __name__ == '__main__':
import doctest
doctest.testmod()
|
...CORRECTION...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | def trouverIndex(t, x):
'''Fonction qui renvoie l'index de l'élément x dans le tableau. None en cas d'échec de la recherche
:: param t(list) :: un tableau contenant le même type d'élément que le paramètre x
:: param x(au choix) :: l'élément qu'on cherche à trouver dans le tableau
:: exemples ::
>>> test = [10,20,30,40,50]
>>> trouverIndex(test, 20)
1
>>> trouverIndex(test, 60)
'''
i = 0
longueur = len(t)
while i < longueur and t[i] != x:
i = i + 1
if i < longueur:
return i
return None # Inutile en réalité : ce serait fait automatiquement
if __name__ == '__main__':
import doctest
doctest.testmod()
|
Phase d'initialisation du TANT QUE
Attention à l'une des erreurs typiques lors de l'utilisation d'une boucle non bornée TANT QUE : le fait d'oublier de donner une valeur par défaut permettant de rentrer dans la boucle à la variable qui gère la boucle.
14
15
16
17 | i = 0
longueur = len(t)
while i < longueur and t[i] != x:
i = i + 1
|
On voit bien que les lignes 14 et 15 permettent de rentrer une première fois dans la boucle.
Sans ces lignes, ça ne peut pas fonctionner.
Conclusion : Ne négligez pas cette phase d'initialisation.
3 - Preuve de terminaison ou preuve d'arrêt
Prouver qu'un algorithme sans récursivité (sans que l'algorithme ne s'appelle lui-même à l'intérieur de l'algorithme) s'arrête pour toutes ENTREES correctement fournies revient au final à prouver que la boucle ne s'exécutera qu'un nombre fini de fois.
Variant de boucle
Pour prouver qu'une boucle non bornée (Tant que) s'arrête, il faut montrer
- que la condition de poursuite de la boucle est de type
while un > 0et - que la suite
unest une suite - à valeurs entières
- strictement décroissante (on est certain que la valeur diminue à chaque boucle)
- positives (on a bien une valeur supérieure à 0 au début) si on veut savoir si elle s'effectue au moins une fois
Cette suite un est ce qu'on nomme le variant de boucle.
Dans ce cas, le variant va nécessairement décroitre et devenir à un moment négatif ou nul. Par contre, si on veut que la boucle soit parcourue au moins une fois, le variant doit bien être initialement positif.
L'arrêt est donc obligatoire au bout d'un certain nombre de bouclages si on peut écrire la condition sous une forme semblable à :
1 | while un > 0:
|
Prouver la terminaison d'un algorithme revient donc à dire qu'on est certain que l'algorithme va s'arrêter quelque soit l'entrée (pourvu que l'entrée respecte les préconditions bien entendu).
Si on ne peut pas prouver sa terminaison, cela ne veut pas dire qu'il va tourner en boucle. Cela veut dire que c'est possible. Or, même s'il n'y a que 0,1% des entrées qui provoquent une boucle infinie, cela veut quand même dire que l'algorithme peut potentiellement provoquer un blocage. Vous prendriez l'avion dans ces conditions ?
Exemple
Prenons ce court programme :
1
2
3 | x = 3
while x < 100:
x = x + 10
|
Etape 1 : avant de rentrer dans la boucle
Ligne 1 : on voit que x vaut 3 initialement.
1 | x = 3
|
Comme nous avons fait 0 tour de boucle TANT QUE, nous noterons ceci :
x0 = 3 |
(1) |
Etape 2 : que se passe-t-il à chaque tour de boucle ?
Ligne 3 : on voit qu'on augmente x de 10 à chaque tour de boucle. La raison vaut donc +10.
3 | x = x + 10
|
On peut donc écrire que x après n+1 tours de boucles vaut x après n tours plus 10.
xN+1 = xN + 10
Nous avons donc affaire à une suite xN arithmétique de raison r = +10 et de valeur initiale x0 = 3 (voir (1)).
xN = x0 + r*n
xN = 3 + 10*n
On obtient donc :
xN = 3 + 10*n |
(2) |
Etape 3 : recherche du VARIANT
On cherche à voir si la condition de boucle de la ligne 2 peut s'écrire sous cette forme :
L2 | while un > 0:
|
On commence la démonstration en récupérant la condition de boucle réelle et on tente de la ramener à la forme attendue pour prouver la terminaison :
L2 | while x < 100:
|
On remplace donc x par xN et on en tente de revenir à la forme attendue.
L2 | while xN < 100:
|
On remplace xN en utilisant (2) :
L2 | while (3 + 10*n) < 100:
|
Pour revenir à la forme attendue, on écrit b > a plutôt que a < b :
L2 | while (3 + 10*n) < 100:
|
L2 | while 100 > (3 + 10*n):
|
Pour revenir à la forme attendue, on doit passer les termes de droite à gauche :
L2 | while 100 > ( + 3 + (10*n) ):
|
L2 | while ( 100 - 3 - (10*n) ) > 0:
|
L2 | while (97 - 10*n) > 0:
|
Nous obtenons alors le VARIANT de boucle uN exprimé de cette façon :
L2 | while uN > 0: avec uN = (97 - 10*n)
|
Etape 4 : conclusion
On voit que le variant est une suite d'entiers dont la raison est r = -10 : on perd 10 à chaque fois. La suite est donc décroissante.
Nous obtenons donc bien
- une condition du type
while uN > 0 - avec
uN = 97 - 10*nune suite d'entiers strictement décroissante.
Nous venons donc de prouver la terminaison de cette boucle.
07° Prouver la terminaison (ou non) du programme ci-dessous. Il faudra trouver un variant qui soit une suite d'entiers positifs strictement décroissante et montrer que la condition du TANT QUE revient à écrire : TANT QUE un > 0
1
2
3
4
5
6
7
8
9 | def exercice(seuil):
'''Fonction-exercice qui ne sert à rien
:: param seuil(int) :: un entier positif
:: return (int) :: un résultat
'''
x = 0
while 5*x < seuil:
x = x + 1
return x
|
...CORRECTION...
Etape 1 : avant de rentrer dans la boucle
Ligne 6 : on voit que x vaut 0 initialement.
6 | x = 0
|
Comme nous avons fait 0 tour de boucle TANT QUE, nous noterons ceci :
x0 = 0 |
(1) |
Etape 2 : que se passe-t-il à chaque tour de boucle ?
Ligne 8 : on voit qu'on augmente x de 1 à chaque tour de boucle. La raison vaut donc +1.
8 | x = x + 1
|
On peut donc écrire que x après n+1 tours de boucles vaut x après n tours plus 1.
xN+1 = xN + 1
Nous avons donc affaire à une suite xN arithmétique de raison r = +1 et de valeur initiale x0 = 0 (voir (1)).
xN = x0 + r*n
xN = 0 + 1*n
On obtient donc juste :
xN = n |
(2) |
Etape 3 : recherche du VARIANT
On cherche à voir si la condition de boucle de la ligne 7 peut s'écrire sous cette forme :
L7 | while un > 0:
|
On commence la démonstration en récupérant la condition de boucle réelle et on tente de la ramener à la forme attendue pour prouver la terminaison :
L7 | while 5*x < seuil:
|
On remplace donc x par xN et on en tente de revenir à la forme attendue.
L7 | while 5*xN < seuil:
|
On remplace xN en utilisant (2) :
L7 | while 5*n < seuil:
|
Pour revenir à la forme attendue, on écrit b > a plutôt que a < b :
L7 | while 5*n < seuil:
|
L7 | while seuil > 5*n:
|
Pour revenir à la forme attendue, on doit passer les termes de droite à gauche :
L7 | while seuil > + 5*n:
|
L7 | while (seuil - 5*n) > 0:
|
Nous obtenons alors le VARIANT de boucle uN exprimé de cette façon :
L2 | while uN > 0: avec uN = seuil - 5*n
|
Etape 4 : conclusion
On voit que le variant est une suite d'entiers dont la raison est r = -5 : on perd 5 à chaque fois. La suite est donc décroissante.
Nous obtenons donc bien
- une condition du type
while uN > 0 - avec
uN = seuil - 5*nune suite d'entiers strictement décroissante.
Nous venons donc de prouver la terminaison de cette boucle.
08° Prouver la terminaison (ou non) du programme ci-dessous. Il faudra trouver un variant qui soit une suite strictement décroissante d'entiers positifs et montrer que la condition du TANT QUE revient à écrire : TANT QUE un > 0
1
2
3
4
5
6
7
8
9 | def exercice(seuil):
'''Fonction-exercice qui ne sert à rien
:: param seuil(int) :: un entier positif
:: return (int) :: un résultat
'''
x = 0
while 5*x < seuil:
x = x - 1
return x
|
...CORRECTION...
Etape 1 : avant de rentrer dans la boucle
Ligne 6 : on voit que x vaut 0 initialement.
6 | x = 0
|
Comme nous avons fait 0 tour de boucle TANT QUE, nous noterons ceci :
x0 = 0 |
(1) |
Etape 2 : que se passe-t-il à chaque tour de boucle ?
Ligne 8 : on voit qu'on diminue x de 1 à chaque tour de boucle. La raison vaut donc -1.
8 | x = x - 1
|
On peut donc écrire que x après n+1 tours de boucles vaut x après n tours plus 1.
xN+1 = xN - 1
Nous avons donc affaire à une suite xN arithmétique de raison r = -1 et de valeur initiale x0 = 0 (voir (1)).
xN = x0 + r*n
xN = 0 - 1*n
On obtient donc juste :
xN = -n |
(2) |
Etape 3 : recherche du VARIANT
On cherche à voir si la condition de boucle de la ligne 7 peut s'écrire sous cette forme :
L7 | while un > 0:
|
On commence la démonstration en récupérant la condition de boucle réelle et on tente de la ramener à la forme attendue pour prouver la terminaison :
L7 | while 5*x < seuil:
|
On remplace donc x par xN et on en tente de revenir à la forme attendue.
L7 | while 5*xN < seuil:
|
On remplace xN en utilisant (2) :
L7 | while 5*(-n) < seuil:
|
L7 | while -5*n < seuil:
|
Pour revenir à la forme attendue, on écrit b > a plutôt que a < b :
L7 | while -5*n < seuil:
|
L7 | while seuil > - 5*n:
|
Pour revenir à la forme attendue, on doit passer les termes de droite à gauche :
L7 | while seuil > - 5*n:
|
L7 | while (seuil + 5*n) > 0:
|
Nous obtenons alors le VARIANT de boucle uN exprimé de cette façon :
L2 | while uN > 0: avec uN = seuil + 5*n
|
Etape 4 : conclusion
On voit que le variant est une suite d'entiers dont la raison est r = +5 : on gagne 5 à chaque fois. La suite est donc croissante.
Nous obtenons donc
- une condition du type
while uN > 0 - mais avec
uN = seuil + 5*nune suite d'entiers strictement croissante.
Nous venons donc de prouver que cet algorithme ne s'arrête pas nécessairement. D'ailleurs la seule manière qu'il s'arrête est que le seuil soit négatif dès le départ.
Alors, notre algorithme de recherche linéaire, consistant à lire les éléments un à un jusqu'à trouver le bon se termine-t-il ?
09° Prouver la terminaison (ou non) du programme de recherche linéaire. Il faudra trouver un variant qui soit une suite strictement décroissante d'entiers positifs et montrer que la condition du TANT QUE revient à écrire : TANT QUE un > 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | def trouverIndex(t, x):
'''Fonction qui renvoie l'index de l'élément x dans le tableau. None en cas d'échec de la recherche
:: param t(list) :: un tableau contenant le même type d'élément que le paramètre x
:: param x(au choix) :: l'élément qu'on cherche à trouver dans le tableau
:: exemples ::
>>> test = [10,20,30,40,50]
>>> trouverIndex(test, 20)
1
>>> trouverIndex(test, 60)
'''
i = 0
longueur = len(t)
while i < longueur and t[i] != x:
i = i + 1
if i < longueur:
return i
return None # Inutile en réalité : ce serait fait automatiquement
if __name__ == '__main__':
import doctest
doctest.testmod()
|
...CORRECTION...
Etape 0 : simplification
La condition de poursuite du TANT QUE se compose de deux conditions associées via un ET. On ne peut continuer que si les deux conditions sont vraies. Cela veut dire qu'on s'arrête dès qu'une des deux conditions est fausse.
Nous allons donc simplifier l'étude en commençant à regarder simplement l'arrêt à l'aide de la première condition. Si nous prouvons l'arrêt, l'algorithme s'arretera également si on lui donne encore plus de raisons de stopper la boucle non bornée.
Mettons de côté la seconde condition de poursuite t[i] != x.
On ne gardera que cela :
16 | while i < longueur:
|
Etape 1 : avant de rentrer dans la boucle
Ligne 14 : on voit que i vaut 0 initialement.
14 | i = 0
|
Comme nous avons fait 0 tour de boucle TANT QUE, nous noterons ceci :
i0 = 0 |
(1) |
Etape 2 : que se passe-t-il à chaque tour de boucle ?
Ligne 17 : on voit qu'on augmente i de 1 à chaque tour de boucle. La raison vaut donc +1.
17 | i = i + 1
|
On peut donc écrire que i après n+1 tours de boucles vaut i après n tours plus 1.
iN+1 = iN + 1
Nous avons donc affaire à une suite iN arithmétique de raison r = +1 et de valeur initiale i0 = 0 (voir (1)).
iN = i0 + r*n
iN = 0 + 1*n
On obtient donc juste :
iN = n |
(2) |
Etape 3 : recherche du VARIANT
On cherche à voir si la condition de boucle de la ligne 16 peut s'écrire sous cette forme :
L16? | while un > 0:
|
On commence la démonstration en récupérant la condition de boucle réelle et on tente de la ramener à la forme attendue pour prouver la terminaison :
L16 | while i < longueur:
|
On remplace donc i par iN et on en tente de revenir à la forme attendue.
L16 | while iN < longueur:
|
On remplace iN en utilisant (2) :
L16 | while n < longueur:
|
Pour revenir à la forme attendue, on écrit b > a plutôt que a < b :
L16 | while n < longueur:
|
L16 | while longueur > n:
|
Pour revenir à la forme attendue, on doit passer les termes de droite à gauche :
L16 | while longueur > + n:
|
L16 | while (longueur - n) > 0:
|
Nous obtenons alors le VARIANT de boucle uN exprimé de cette façon :
L16 | while uN > 0: avec uN = longueur - n
|
Etape 4 : conclusion
On voit que le variant est une suite d'entiers dont la raison est r = -1 : on perd 1 à chaque fois. La suite est donc décroissante.
Nous obtenons donc bien
- une condition du type
while uN > 0 - avec
uN = longueur - nune suite d'entiers strictement décroissante.
Nous venons donc de prouver la terminaison de cette boucle.
Puisqu'il s'agit de la seule boucle de cette fonction, on peut en déduire que la fonction se termine également.
La condition peut s'écrire de la façon suivante :
7 | while 0 < (longueur - index):
|
7 | while (longueur - index) > 0:
|
Soit, on remplaçant x par son expression :
7 | while (longueur - n) > 0:
|
Nous avons une condition TANT QUE un > 0 basée sur une suite décroissante d'entiers positifs.
Nuos venons de prouver que la boucle se termine.
4 - Coût et Complexicité
Voyons maintenant comment comparer des algorithmes entre eux.
Nous allons étudier ce qu'on appelle la complexité de l'algorithme. On parle également de coût de l'algorithme.
Le coût d'un algorithme est le nombre d'opérations élémentaires (arithmétiques ou logiquess) ainsi que d'affectations nécessaires à son exécution.
Il s'agit de voir comment va évoluer le nombre d'instructions ou le nombre d'évaluations à effectuer lorsque le nombre de données d'entrée n évolue.
On comprend bien qu'il vaut mieux que ce nombre d'instructions soit lié à n qu'à n2 ou pire 2n.

On voit que la fonction 2n donne un nombre énorme d'instructions à effectuer.
Le but est donc de créer des algorithmes qui demandent le moins d'opérations possibles.
Tentons de trouver la complexité de notre algorithme de recherche.
Le plus facile est de tenter de trouver cette complexité dans le pire des cas. Puisque la méthode consiste à lire les éléments un par un dans l'ordre, le pire des cas est ici que l'élément cherché n'existe pas dans le tableau. Il faudra alors parcourir tout le tableau.
Voici donc le programme dans lequel j'ai simplement rajouté un print de façon à connaitre la valeur de l'index juste avant que la fonction ne réponde. Comme cela, on connaitre le nombre de fois où la boucle a été effectuée.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | def trouverIndex(tableau, x):
'''Fonction qui renvoie l'index de l'élément x dans le tableau. None en cas d'échec de la recherche
:: param t(list) :: un tableau contenant le même type d'élément que le paramètre x
:: param x(au choix) :: l'élément qu'on cherche à trouver dans le tableau
'''
i = 0
longueur = len(t)
while i < longueur and t[i] != x:
i = i + 1
print(i)
if i < longueur:
return i
return None # Inutile en réalité : ce serait fait automatiquement
|
10° Placer la fonction en mémoire dans votre éditeur.
Utiliser les commandes suivantes dans le Shell. Le fait d'avoir placé un print dans la fonction permet de connaitre le nombre de boucles ayant été effectuées avant de sortir de la fonction.
Répondre à la question suivante : lorsqu'on fournit à cet algorithme un tableau de n éléments, la complexité de cet algorithme de recherche est-il lié à n (linéaire), n2 (quadratique) ou à n3 (cubique) ?
On remarquera que lors de tous les tests, on fait une recherche sur un élément inexistant de façon à devoir parcourir tout le tableau.
>>> valeurs = [x for x in range(100)]
>>> rep = trouverIndex(valeurs, -10)
>>> valeurs = [x for x in range(1000)]
>>> rep = trouverIndex(valeurs, -10)
>>> valeurs = [x for x in range(10000)]
>>> rep = trouverIndex(valeurs, -10)
...CORRECTION...
Dans tout les cas, on a 2 affectations avant la boucle : i = 0 et longueur = len(t)
Dans la boucle :
- 100 données, 100 boucles.
- 1000 données, 1000 boucles.
- 10000 données, 10000 boucles.
On voit donc clairement que la complexité est linéaire, pour n, on a n + 2
C'est à dire en n.
5 - Notations O et Θ (culture générale)
Ces notations ne font pas partie explicitement du programme. Néanmoins, la recherche de coût revient en réalité à étudier ces notions. Je présente donc ici deux notations intéressantes, mais il en existe d'autres.
Commençons par voir la notation O (qu'on prononce GRAND O) qui permet de définir une borne supérieure au comportement d'un algorithme.
Définition simplifiée de la notation O : borne supérieure du coût de l'algorithme
Pour comparer les complexités des algorithmes entre eux, on utilise la notation suivante par exemple :
f(n) = O(n2) indique que le coût de la fonction f(n) est au maximum égal à n2 mais qu'il est possible qu'il soit en réalité plus performant que cela (en n, en n1/2 ou en log2 n par exemple).
Exemple
- si on écrit f(n) = O(2n), cela veut dire que notre algorithme évolue en 2n ou mieux : en n4, ou en n3...)
- si on écrit f(n) = O(n4), cela veut dire que notre algorithme évolue en n4 ou mieux : en n3, en n2, en n...)
- si on écrit f(n) = O(n3), cela veut dire que notre algorithme évolue en n3 ou mieux : en n2, en n, en n1/2...)
- si on écrit f(n) = O(n2), cela veut dire que notre algorithme évolue en n2 ou mieux : en n, en n1/2, en log2 n...)
On peut également en tirer des informations sur ce que le coût n'est pas : f(n) = O(n4) implique qu'on est certain que notre algorithme n'est pas en 2n ou n5.
Par contre, on ne sait pas s'il est réellement n4, en n3 ou encore moins.
Parfois, on connait mieux l'algorithme que cela. On peut prévoir comment il réagit vraiment et pas juste donner une borne supérieure à son comportement. On utilise alors la notation Θ (on prononce Theta).
Notation Θ : ordre de grandeur du coût
Pour comparer les complexités des algorithmes entre eux, on utilise la notation suivante par exemple :
f(n) = Θ(n2) indique que la fonction f(n) se comporte d'une façon similaire à n2 pour les grandes valeurs de n.
Si f(n) = 4 n2 + 100 n, on doit écrire f(n) = Θ(n2) uniquement.
Si f(n) = 12 n3 - 500 n, on doit écrire f(n) = Θ(n3) uniquement.
11° Trouver le coût des algorithmes dont on vous donne l'expression mathématique du nombre d'opérations à effectuer en fonction du nombre n de données d'entrée.
f(n) = 10 n4 + 3 n2 + 4000 n
f(n) = 300 n3 + 9000 n2 + 10 n
f(n) = 9000 n2 + 10 n
... CORRECTION ...
f(n) = 10 n4 + 3 n2 + 4000 n
On voit que f(n) évolue comme une fonction n4.
On peut écrire f(n) = Θ(n4).
On pourrait également écrire f(n) = O(n4) mais également f(n) = O(n5) ou pire : f(n) = O(2n)...
f(n) = 300 n3 + 9000 n2 + 10 n
On voit que f(n) évolue comme une fonction n3.
On peut écrire f(n) = Θ(n3).
f(n) = 9000 n2 + 10 n
On voit que f(n) évolue comme une fonction n2.
On peut écrire f(n) = Θ(n2).
Activité publiée le 12 02 2021
Modifié le : 28 02 2021
Auteur : Andjekel
Source : Infoforall - ows. h.